
Logiciel ou programme - Stratégie - Exemples
1 - Programmes proposés : Présentation - Téléchargement (Windows, Mac OS, Linux).
2 - Article PDF de présentation de ce logiciel et sur ses applications pédagogiques possibles.
3 - Exemples de débuts de parties.
4 - Au sujet des jeux de NIM.
5 - Liens interessants.
6 - Autres programmes du même auteur.
Vous aimez les jeux d’allumettes !
Voici des programmes pour deux d'entre eux, classiques. Ils se jouent à 2 joueurs. Ici, vous et la machine .
1 - Basique : avec un seul tas d’allumettes. On en prend 1, 2 ou 3 à chaque coup.
Pour les experts, il y a possibilité de faire varier les données du jeu. On peut ainsi paramétrer des jeux décroissants ou croissants. Une option permet au joueur de bénéficier d'une aide visuelle et numérique (ce qui permet de mettre en évidence la stratégie gagnante).
2 - Marienbad : avec plusieurs tas. On prend autant d’allumettes qu’on veut, mais dans un seul tas.
Là aussi, pour les experts, on peut faire varier les données. Une option permet d'afficher les nombres d'allumettes des paquets en numération binaire en alignant les unités (ce qui permet d'expliquer la stratégie gagnante).
Téléchargement d'un setup d'installation des 2 programmes pour Windows :
Solution recommandée, la plus pratique.
https://alainb-sites.fr/NIM/setup_NIM.zip
C’est un fichier zip qui une fois décompressé donne unsetup.exe
Celui-ci installe les 2 programmes de jeux, leur aide en ligne et un readme dans un groupe de programmes (NIM).
Il place aussi des raccourcis des 2 programmes sur le bureau.
On peut choisir les emplacements des fichiers.
On lance les programmes en cliquant dans le groupe ou sur les raccourcis.
Les programmes sont seulement copiés dans un dossier et ne touchent pas au système Windows.
On désinstalle le tout comme n’importe quel programme windows.
Téléchargement des éxécutables (.exe) séparément :
[ Cliquez sur un lien pour télécharger un programme. Placez le sur votre bureau par exemple. Il suffit de double-cliquer dessus pour le lancer et pouvoir jouer, sous windows ]
1 - Basique, avec un seul tas d’allumettes.
Pour Windows : https://alainb-sites.fr/NIM/NIM_basique.exe [ Version du : 26/02/2023 ]
Pour Macintosh : https://alainb-sites.fr/NIM/NIM_basique_mac [ Version du : 14/03/2023 ]
Lire les instructions ci-dessous pour pouvoir faire fonctionner ces programmes avec Mac OS.
Pour Linux : https://alainb-sites.fr/NIM/NIM_basique_linux [ Version du : 28/04/2025 - FORMAT ZIP)]
Lire les instructions ci-dessous pour pouvoir faire fonctionner ces programmes avec Linux.
2 - Marienbad, avec plusieurs tas.
Pour Windows : https://alainb-sites.fr/NIM/NIM_Marienbad.exe [ Dernière mise à jour : 22/02/2023 ]
Pour Macintosh : https://alainb-sites.fr/NIM/NIM_Marienbad_mac [ Dernière mise à jour : 14/03/2023 ]
Lire les instructions ci-dessous pour pouvoir faire fonctionner ces programmes avec Mac OS.
Pour Linux : https://alainb-sites.fr/NIM/NIM_Marienbad_linux [ Version du : 28/04/2025 - FORMAT ZIP]
Lire les instructions ci-dessous pour pouvoir faire fonctionner ces programmes avec Linux.
Avec un Mac OS :
Contrairement à Windows, Mac OS ne permet pas d'ouvrir directement un programme téléchargé qu'il ne reconnaît pas. Vous trouverez ci-dessous la procédure à suivre pour pouvoir exécuter les programmes téléchargés sur Mac OS.
Procédure permettant de faire fonctionner les programmes téléchargés sous Mac OS :
– D'abord, télécharger le programme.
– Le placer sur le bureau par exemple.
– Ouvrir l'utilitaire Terminale (il se trouve sur tous les MacIntoshs).
– S'identifier en tant qu'administrateur avec la commande « login ».
Cette commande demande d'abord de rentrer son identifiant, puis son mot de passe. Attention le mot de passe reste invisible lors de sa saisie.
– Se placer dans le répertoire où se trouve le ou les programmes grâce à la commande « cd ».
Par exemple, dans notre cas : « cd /users/nom d’utilisateur/Desktop »
– Puis, entrer la commande : « chmod 755 », suivie du nom du fichier.
Une fois la commande exécutée l'icône du fichier prend la couleur noire de celui du Terminale.
– Pour le premier lancement du programme, cliquez sur son icône en appuyant en même temps sur la touche contrôle (Ctrl) et choisir « ouvrir » dans le menu déroulant qui apparaît. Puis, confirmer l'ouverture du programme. Le programme s'ouvre dans la fenêtre du Terminale.
– Pour les fois suivantes, il suffira de double-cliquer sur l'icône du programme pour l’ouvrir.
Toutes ces manipulations ne se font qu'une fois pour un même programme.
La fenêtre par défaut du Terminale, ainsi que les polices qu'il utilise et ses couleurs sont paramétrables dans le sous menu « Paramètres » du menu « Terminale ».
Avec Linux :
Linux ne permet pas d'ouvrir directement ces programmes. Il faut passer par la console du terminal. Vous trouverez ci-dessous la procédure à suivre pour pouvoir exécuter les programmes téléchargés sous Linux. La compilation et les tests ont été faits avec la distribution d'UBUNTU.
Procédure permettant de faire fonctionner les programmes téléchargés sous Linux :
– D'abord, télécharger le programme Zipé puis le déZiper.
– Le placer sur le bureau par exemple, ou dans un dossier de votre choix.
– Cliquez droit sur l'icone du programme, là ou il se touve. Choisir "propriétés" dans le menu contextuel, puis, sous l'onglet "permissions", côcher la case "autoriser l'éxécution du programme" (si cette case n'est pas déjà cochée).
– Ouvrir l'utilitaire Terminale (il se trouve dans le groupe Utility de la liste des programmes).
– Rentrez la commande /chemin du programme complet/Nom du programme , ou alors ./chemin relatif/nom du programme (le chemin relatif par du répertoire par défaut ou de celui dans lesquel vous vous êtes placé avec la commande cd ). Si vous vous êtes placé dans le répertoire où se trouve le programme, tapez simplement ./nom du programme.
– Le programme devrait se lancer alors dans la fenêtre du terminal.
Exemples de débuts de parties :
Jeux avec un seul tas :
1 - La forme courante : On démarre avec 16 allumettes. Pour jouer, il faut en enlever 1, 2 ou 3. Celui qui prend la dernière à gagné ici. Le joueur commence.
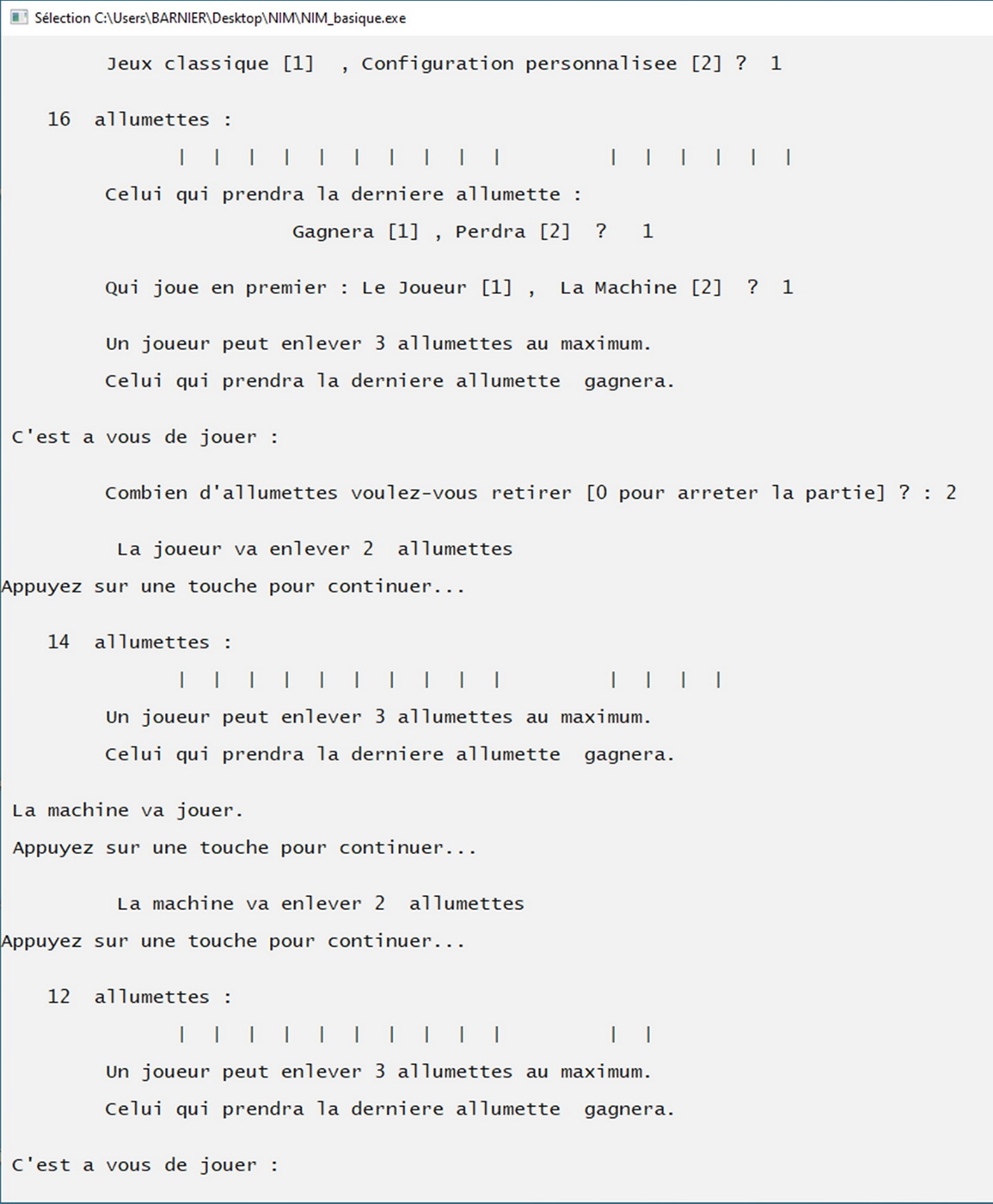
2 - Une configuration personnalisée décroissante : On démarre avec 25 allumettes. Pour jouer, il faut en enlever 4 au maximum, mais au moins une. Le premier qui entamera les 4 denières allumettes gagnera ici. C'est la machine qui commence.

3 - Une configuration personnalisée croissante : Le départ se fait avec 6 allumettes. Chaque joueur peut en ajouter au plus 7, mais au moins une. Le premier qui atteind la 35 eme à gagné ici. C'est le joueur qui commence.

Une option d'aide permet au joueur de découvrir la stratégie gagnante par l'affichage du tas d'allumette en paquets et celui des calculs associés. Cet affichage s'adapte à tous les cas possibles : jeux décroissants ou croissants avec des nombres de départs et d'arrivées quelconques et un nombre d'allumettes maximum à retirer quelconque également.
4 - Cas classique décroissant : de 16 allumettes à une, avec une prise de 3 maximum à chaque coup. Celui qui prend la dernière, perd.

5 - Cas croissant : de 3 allumettes à 27, avec un jeu maximum de 4. Celui qui atteind 27, gagne.

Jeux avec plusieurs tas :
1 - La configuration classique dite de Marienbad : 4 tas de 1 - 3 - 5 - 7 allumettes. Chaque joueur enlève autant d'allumettes qu'il veut dans un tas de son choix, mais dans un seul. Celui qui prend la dernière allumette perd ici. La machine joue en premier.
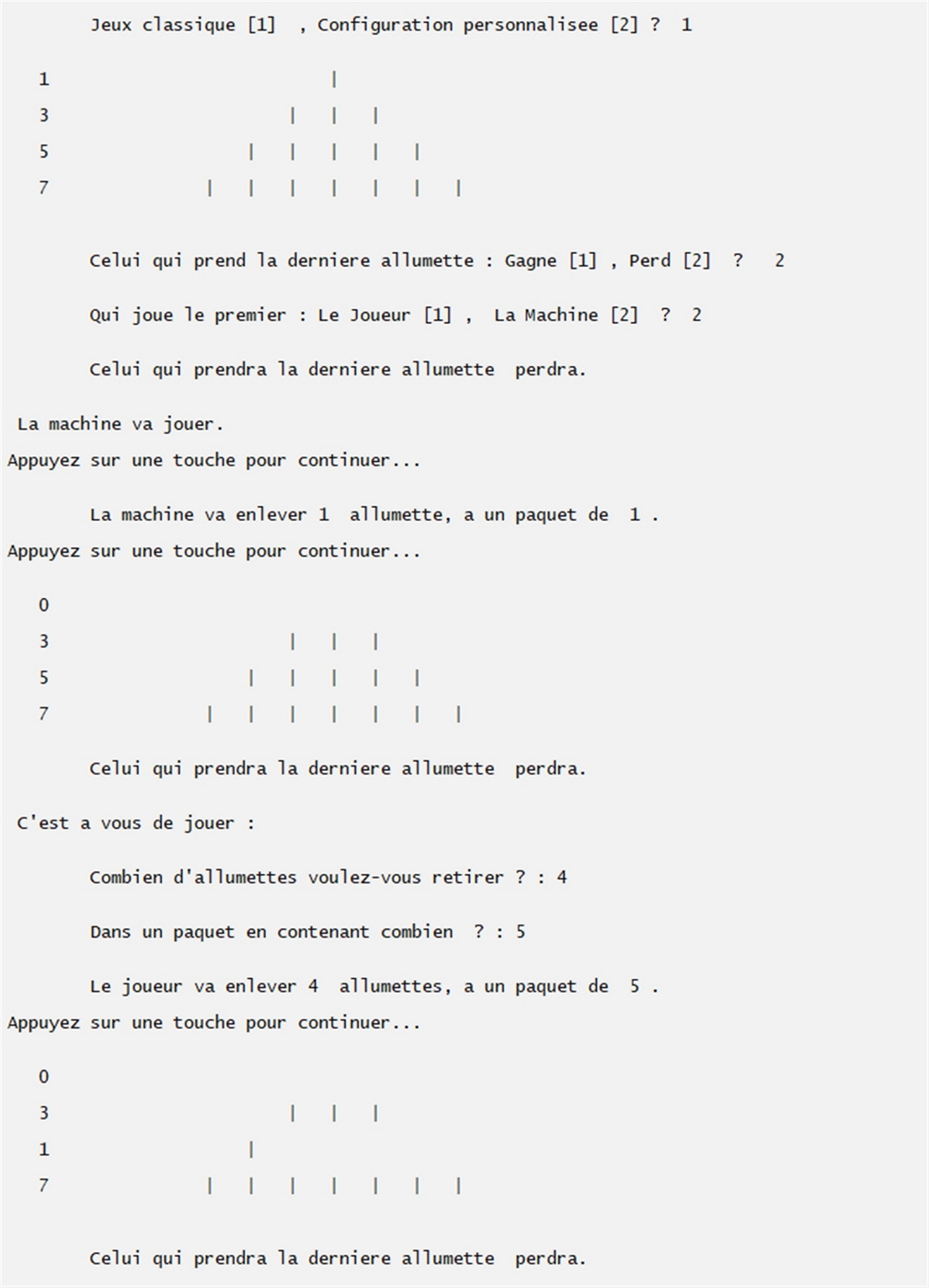
2 - Une configuration personnalisée différente : 5 tas de 9 - 6 - 6 - 7 - 2 allumettes. Chaque joueur enlève autant d'allumettes qu'il veut dans un tas de son choix, mais dans un seul. Le gagnant ici est celui qui prend la dernière. La machine joue le premier coup.

Une option rajoutée, permet d'afficher les nombres d'allumettes des paquets en numération binaire, sur le côté droit du jeu, en alignant les unités. Ceci de façon à pouvoir mettre en évidence la stratégie gagnante basée sur cette écriture. Deux extraits de parties avec cet affichage :
3 - Jeu classique. Celui qui prend la dernière, perd :
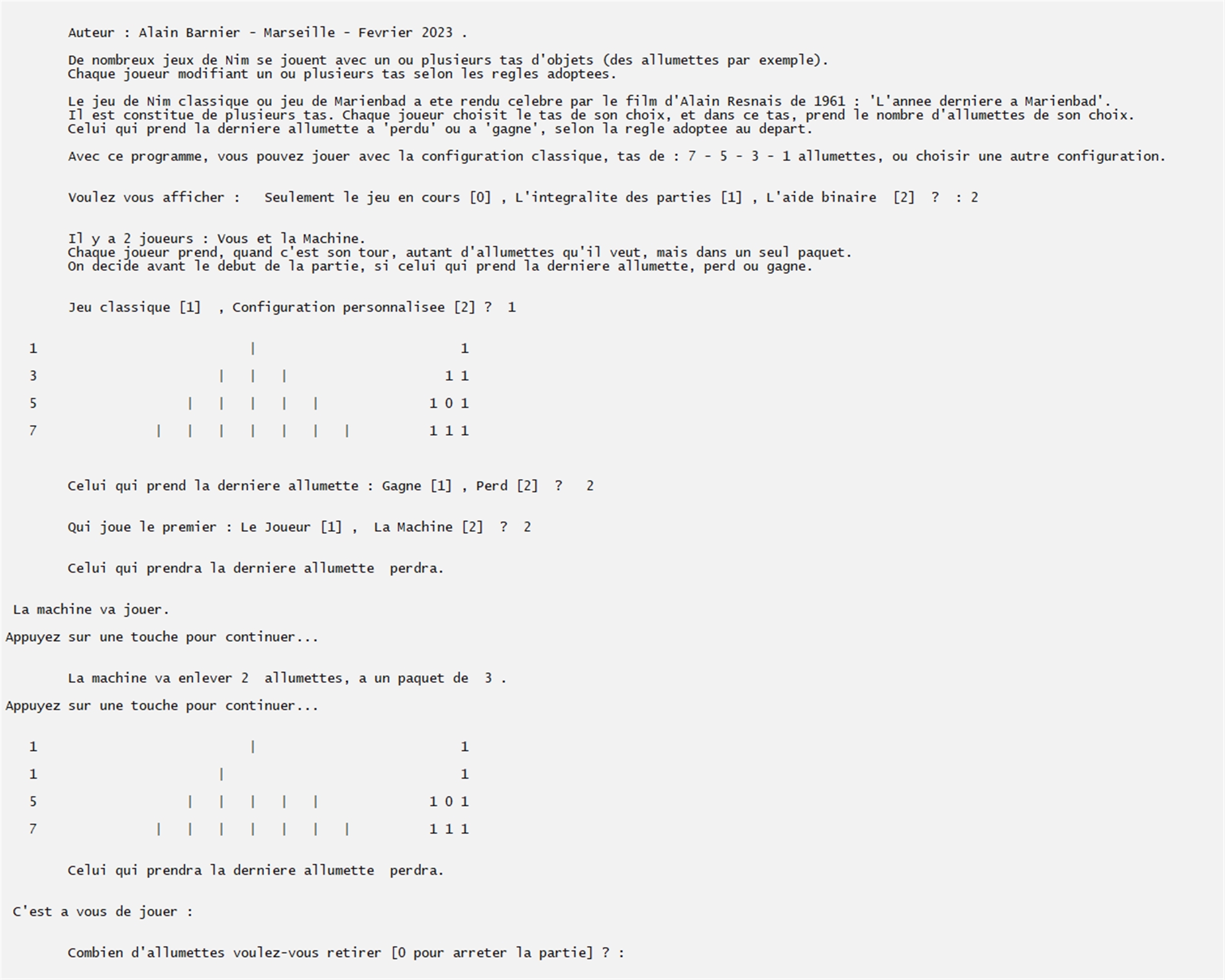
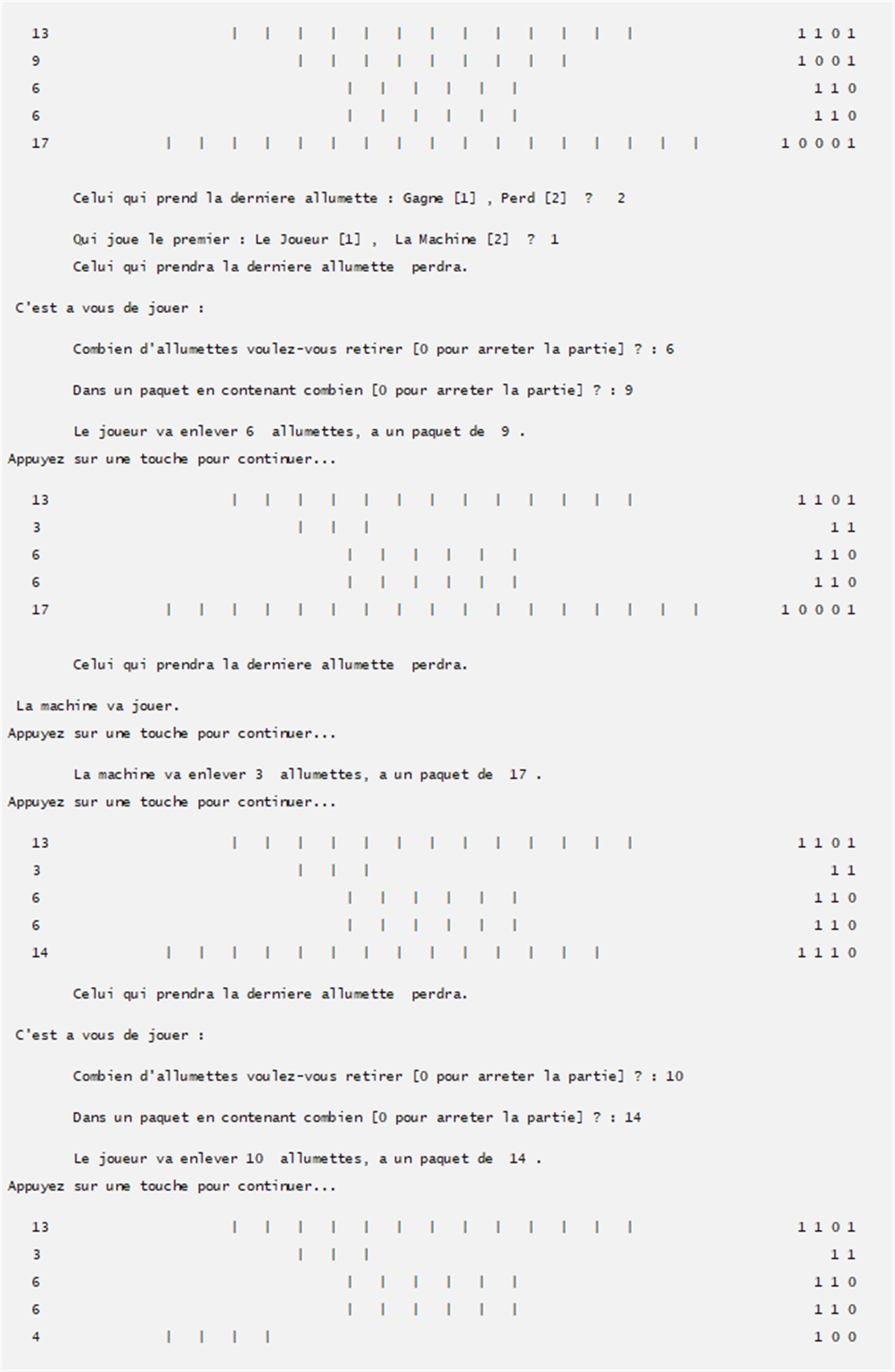
4 - Une configuration de 5 paquets de 13, 9, 6, 61 et 17 allumettes. Celui qui prend la dernière, perd.
Au sujet des jeux de NIM
PRÉSENTATION
Les jeux de Nim sont des jeux de stratégie pure, à deux joueurs, où le hasard n’intervient pas. La principale caractéristique de ce jeu est qu’il est toujours possible de déterminer une stratégie gagnante, soit pour le joueur qui commence la partie, soit pour celui qui joue en second.
Ces jeux, dont il existe d'innombrables variantes, se jouent avec des billes, des jetons, des allumettes, etc.
Il s'agit de prendre, de déplacer ou de poser un certain nombre d'objets ; selon les variantes, le dernier à jouer gagne ou perd. Il y a forcément un gagnant et donc un perdant.
HISTORIQUE
Les origines des jeux de Nim remontent très loin dans le temps, si bien qu'il est impossible d'indiquer avec certitude leur provenance
Ils sont signalés en Chine sous le nom de fan-tan et connus en Afrique sous le nom de tiouk-tiouk. Ils apparaitront en Europe dès le XVIe siècle.
Le nom qu’ils portent actuellement leur a été donné par le mathématicien américain issu de Harvard, Charles Léonard Bouton, qui trouva l’algorithme permettant de gagner à coup sûr et qui publia en 1901 un article dans The Annals of Mathematics intitulé, « Nim, a game with a complete mathematical theory ».
Pour la première fois, ce jeu combinatoire impartial, c'est-à-dire où le hasard n'intervient pas et où les mouvements possibles sont les mêmes pour les deux joueurs, était résolu.
Cependant, nous ne savons pas si Nim provient de l’allemand Nimm qui signifie prendre, ou si c’est une astuce graphique puisqu’en retournant NIM, on obtient le mot anglais WIN qui signifie gagner.
JEU DE NIM À UN SEUL TAS
La forme « normale » du jeu consiste à disposer sur la table un nombre quelconque d’allumettes. Tour à tour, les joueurs A et B peuvent retirer 1 à 3 allumettes. Supposons que le joueur A connaisse la stratégie gagnante : On peut démontrer que lorsque le joueur A laisse sur la table un jeu contenant 4 allumettes à son adversaire B, celui-ci ne peut en prendre qu 1, 2 ou 3, laissant forcément à A la possibilité degagner.
Une fois ce principe compris, il est toujours possible de ramener la situation laissée par l’adversaire B, à une situation gagnante pour le joueur A.
JEU DE NIM CLASSIQUE
Le jeu dit de Marienbad a été popularisé par le film d’Alain Resnais et d'Alain Robbe-Grillet, L'Année dernière à Marienbad, en 1961.
Ce jeu de société combinatoire abstrait, dont il existe plusieurs variantes, se joue avec des graines, des dominos, des jetons, des cartes, des allumettes, ... Son origine est probablement très ancienne. Il appartient à la famille plus large des jeux de Nim.
Cette variante a été rendue célèbre par le film d'Alain Resnais au point d'en prendre le nom. Dans ce film, l'un des protagonistes gagne parties sur parties. Il prononce cette phrase à la portée symbolique : Je peux perdre, mais je gagne toujours...
Dans la version du film, il y a quatre rangées, avec respectivement 1, 3, 5, 7 allumettes et celui qui prend la dernière allumette perd. À chaque tour, le joueur prend le nombre d'allumettes qu'il veut, au moins une et dans une même rangée. Dans une autre variante, le gagnant est celui qui prend la dernière allumette.
Plus généralement, le jeu de Nim se joue avec plusieurs tas composés chacun de plusieurs allumettes disposées en pyramide ou en ligne. Chaque joueur, à tour de rôle, peut enlever autant d’allumettes qu'il le souhaite, mais dans un seul tas à la fois. Le gagnant est celui qui parvient à retirer la dernière allumette. Dans la version « misère », celui qui prend la dernière allumette a perdu.
Intéressons-nous maintenant à la stratégie gagnante, découverte par Charles Bouton. Celui-ci démontre qu’un joueur dans une position favorable possédait toujours un coup qui lui permettait de gagner, alors que le joueur en situation défavorable, peu importe le coup qu’il jouait,ne pouvait se retrouver dans une situation gagnante.
Pour bien comprendre le théorème de Bouton, il est nécessaire de comprendre l’écriture en base 2 car il repose en grande partie dessus.
Voici quelques liens intéressants sur ce type de jeux :
Wikipédia : https://fr.wikipedia.org/wiki/Jeux_de_Nim
Technique : https://interstices.info/jeux-de-nim/
Pédagogique : https://www.mathenjeans.fr/mots-cles-sujets-et-publications/jeu-de-nim
Autres programmes du même auteur
https://developer.apple.com/services-account/download?path=/Developer_Tools/Xcode_13.2_beta/Xcode_13.2_beta.xip