Mathématiques et Informatique  

  Sommes  Harmoniques  et  de  KEMPNER  

 

Table des matières

 

 

INTRODUCTION

 

La suite harmonique est la suite des inverses des entiers naturels : 1 , 1/2 , 1/3 , 1/4 , 1/5 , ......

Arrétons nous a 1/N et faisons la somme des termes de la suite. Appelons H(N) cette somme.

H(N) = 1 + 1/2 + 1/3 + 1/4 + 1/5 + .... + 1/N.

On démontre de plusieurs façons que la série ainsi obtenue diverge. Dans notre cas, c'est dire que la somme H(N) tend vers l'infini quand N tend vers l'infini (alors que le dernier terme 1/N tend vers zéro).

On peut constater que cette divergence est trés lente (la vitesse de divergence  est trés comparable à la vitesse à laquelle ln(N) tend vers l'infini avec N).

Quand on supprime une certaine catégorie de termes de la suite on obtient des séries dont certaines sont convergentes.

C'est le cas de la série de Kempner obtenue à partir de la série Harmonique en supprimant tous les termes de la suite dont le dénominateur contient le chiffre 9.

Cette série converge, mais trés lentement.

Les programmes décrits et commentés ci-dessous permettent de calculer, en employant plusieurs techniques, des valeurs approchées ou exactes des sommes des termes de ces suites jusqu'au terme 1/N.

On peut ainsi se rendre compte de leurs  vitesses de divergence ou de convergence.

 

 

 

Présentation et mode d'emploie des programmes

 

Ce programme permet de :

1)   Calculer la somme H(N) des termes de la suite harmonique jusqu'au terme 1/N. La valeur de N est demandée en entrée.

Il permet d'envisager le cas de suites dites « normales » et de suites dites « paires » ou « impaires ».

Pour les sommes « paires » ou « impaires »,  on ne garde de la suite « normale » que les termes dont les dénominateurs sont respectivement pairs ou impairs. Le dernier dénominateur N devant être lui-même pair ou impair. La suite « normale » de dernier terme 1/N en comprend N, tandis que la suite « paire » en comprend N/2 et que la suite « impaire » à (N +1)/2 termes. Le programme indique dans tous les cas ce nombre de termes.

Pour cette partie du programme la somme H(N) est determinée de proche en proche.

La valeur de H(N) est donnée sous  forme décimale approchée ou sous sa forme fractionnaire exacte.

On peut afficher facultativement sa valeur exacte sous la forme d'une fraction P/Q irréductible  (***).

La dernière version du programme  permet d'afficher plus rapidement une valeur approchée de la somme pour de grandes valeurs de N, sans en calculer la valeur exacte.

Pour les valeurs approchées on peut choisir librement leur nombre de chiffres significatifs exacts (Il peut-être trés grand et quelque soit le mode de calcul les résultats sont identiques).

Le programme propose pour calculer les sommes exactes de regrouper les termes en "paquets". Il calcule les valeurs fractionnaires exactes de ces paquets. Il  effectue ensuite leur somme fractionnaire exacte ainsi que la somme de leurs valeurs approchées. Cette façon de regrouper les termes en "paquets" permet, dans certains cas, de raccourcir les temps de calcul.

Le calcul de la valeur approchée d'une somme harmonique de dernier terme 1/N n'utilise pas ici la formule d'EULER-MASCHERONI - Voir la remarque de Gérard Lopez  plus loin   (**)  -  La partie 4  du programme permet d'obtenir ce résultat trés rapidement et pour de plus grandes valeurs de N, en utilisant cette formule ou développement.

La fraction exacte une fois affichée, il est possible d'obtenir les factorisations de P et Q.

Ne choisir ces deux dernières options que pour des valeurs "raisonnables" de P et Q.

La somme effectuée pour une valeur 1/N du dernier terme, on peut la compléter pour une autre valeur de 1/N avec N plus grand.

Les valeurs entières de P et Q deviennent vite trés grandes quand N croit, jusqu'à saturer la mémoire des ordinateurs.

Les calculs des valeurs approchées de sommes harmoniques dans différents cas permettent de se rendre compte du fait que la série harmonique divergent extrèmement lentement et d'estimer, démonstrations à l'appuie, la vitesse de cette divergence  (**).

 

Exemples d'utilisations.

 

            Calculs enchainés :

            1) Calcul d'une somme harmonique complète pour N = 20 sous formes fractionnaire et approchée (6 chiffres significatifs).

 

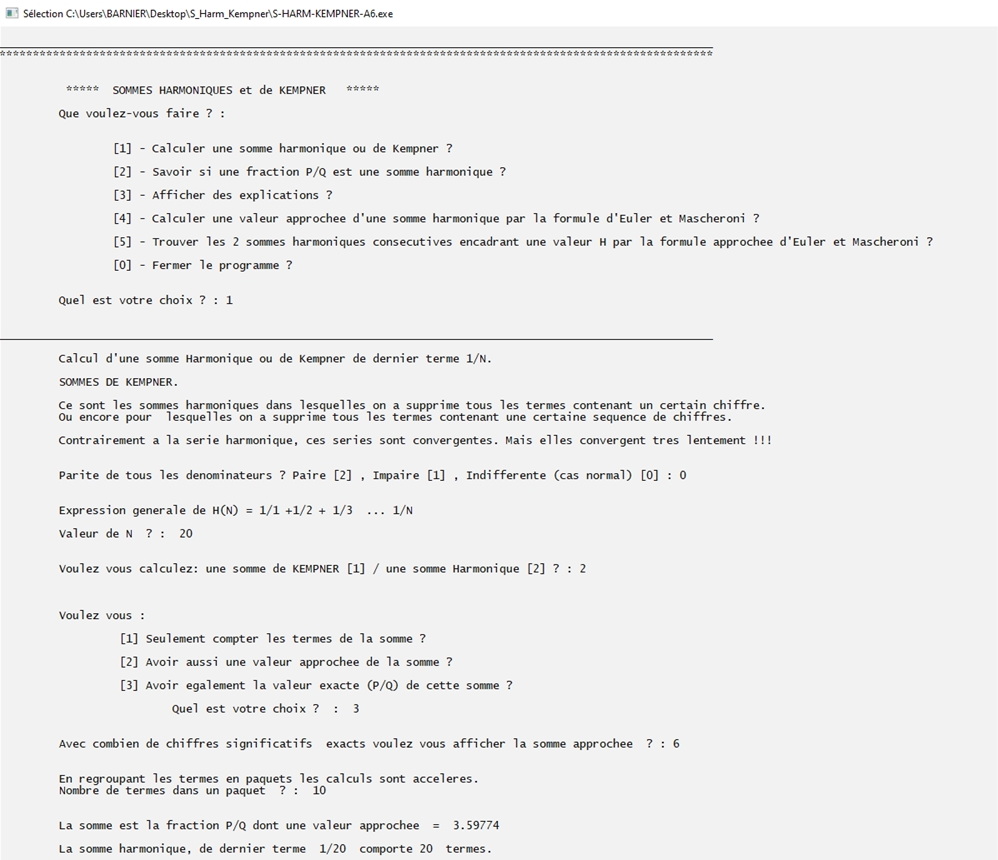
            2) Puis pour 30 termes.

            3) ensuite pour 200 termes, sa valeur approchée seulement.

            4) de même pour 2000 termes.

             5) finalement pour 10 000 termes.

 

 

             Deuxième enchainement de calculs :

             1) Calcul d'une somme paire avec N = 36 (18 termes) sous forme approchée uniquement (20 chiffres significatifs).

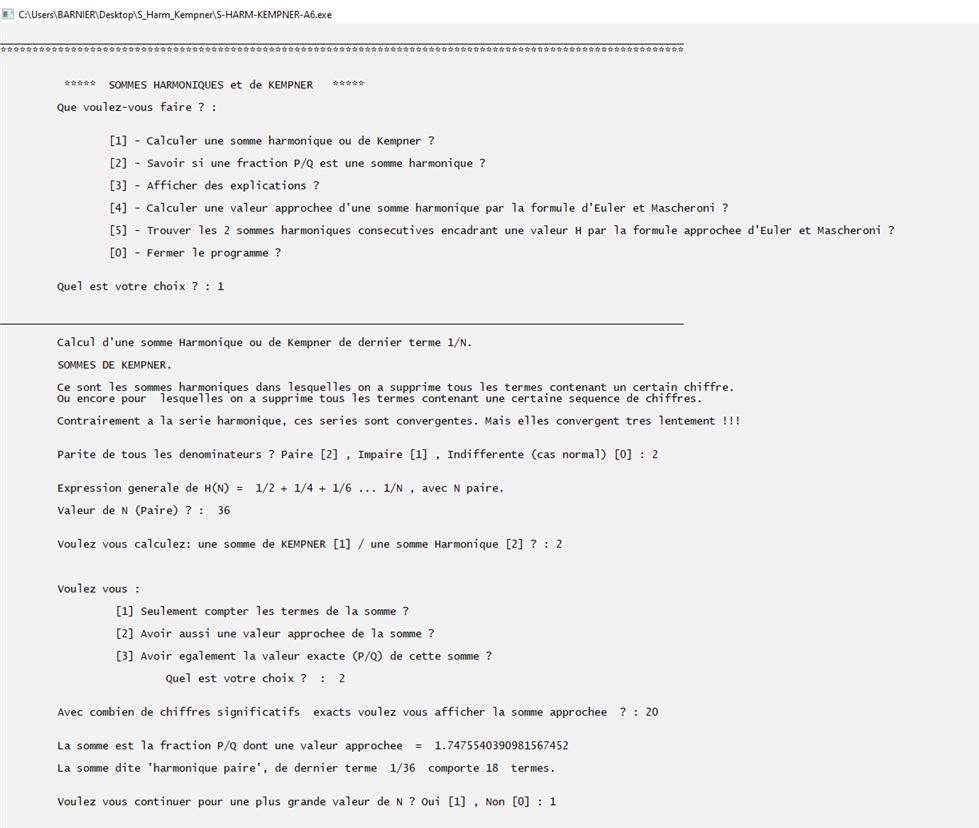
             2) prolongement du calcul pour N = 250 .

            3) puis N = 6000.

             ------------------------------------------------

             Nouveau calcul : somme paire avec N = 36  et affichage de la valeur fractionnaire.

             Prolongement du calcul précèdent avec N à 250.

 

 

 

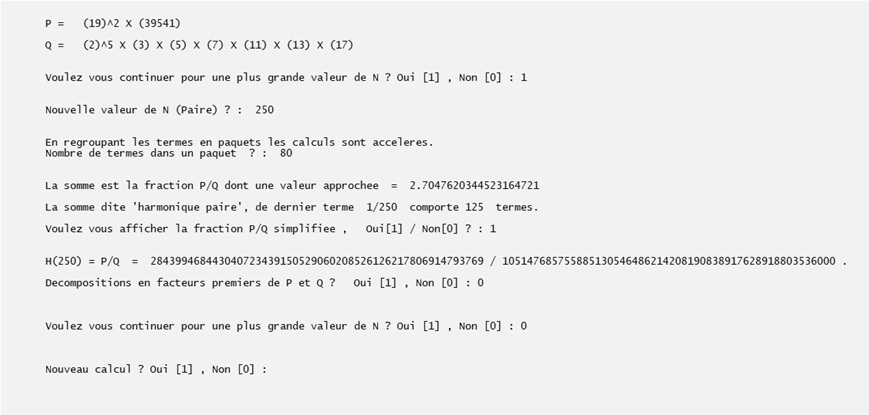
Ce programme permet de :

2)   Calculer une somme de KEMPNER pour une valeur du dernier terme égale ou précédant immédiatement 1/N.

Une somme de KEMPNER est une somme Harmonique dans laquelle on a supprimé tous les termes contenant un chiffre donné ou une séquence de chiffres donnée. Il a été démontré que les sommes de Kempner convergent, contrairement à la série harmonique complète. Mais elles convergent extrémement lentement !

On peut, comme pour la série Harmonique calculer des sommes de Kempner, "Paires" ou "Impaires".

Une valeur N est demandée. Le dernier terme de la somme aura pour dénominateur la plus grande valeur possible égale ou précèdent N.

Une fois les paramètres fixés on peut  choisir de compter les termes de la somme sans en calculer la valeur fractionnaire exacte simplifiée  (*).

Si cette dernière est calculée, une valeur décimale approchée est d'abord affichée.

La dernière version du programme  permet d'afficher plus rapidement une valeur approchée de la somme pour de grandes valeurs de N, sans en calculer la valeur exacte.

Pour les valeurs approchées on peut choisir librement leur nombre de chiffres significatifs exacts (Il peut-être trés grand et quelque soit le mode de calcul les résultats sont identiques).

Le programme propose pour calculer les sommes exactes de regrouper les termes en "paquets". Il calcule les valeurs fractionnaires exactes de ces paquets. Il  effectue ensuite leur somme fractionnaire exacte ainsi que la somme de leurs valeurs approchées. Cette façon de regrouper les termes en "paquets" permet, dans certains cas, de raccourcir les temps de calcul.

La fraction exacte une fois affichée, il est possible d'obtenir les factorisations de P et Q. Ne choisir ces deux dernières options que pour des valeurs "raisonnables" de P et Q.

La somme effectuée jusqu'àu  dernier terme possible précèdant  1/N, on peut la compléter pour une autre valeur de 1/N avec N plus grand.

A titre indicatif, pour une valeur de N de 10 000 000 et en supprimant tous les termes contenant le chiffe "0" il en reste 5 380 839 et la somme vaut environ  12.3537. Il a été prouvée que sa limite quand N tend vers l'infini est voisine de  23,10344… . On est donc loin du compte ! Pour approcher cette somme de plus prés en utilisant ce programme, il faudrait un ordinateur trés rapide avec beaucoup de mémoire vive.

 

 

Exemples d'utilisations.

 

Calcul d'une somme de Kempner obtenue en supprimant tous les termes de la suite harmonique contenant le chiffre 0. 

1) Pour N = 100 avec affichage de la somme fractionnaire exacte et de la valeur approchée à 15 chiffres significatifs.

2) On prolonge la somme pour N = 1000, sans afficher sa valeur fractionnaire.

 

On calcule une nouvelle somme de Kempner obtenue en supprimant tous les termes de la suite harmonique contenant la séquence 0, 2

1) D'abord pour N = 200.

 

             2) Pour N= 200 on affiche la somme fractionnaire exacte et la valeut approchée avec 15 chiffres significatifs.

             3) On continue le calcul pour N= 1000, sans afficher la valeur fractionnaire de la somme.

 

          On calcule maintenant une somme de Kempner impaire dont le dernier terme est égal ou inférieur à 5001.

 

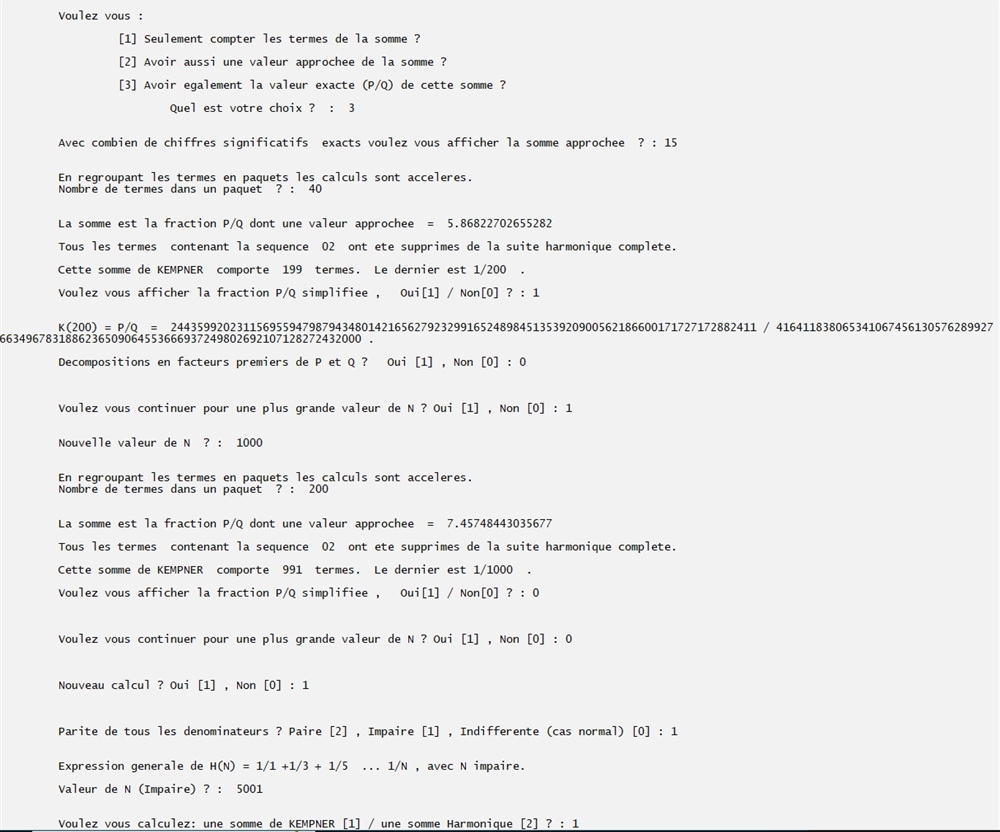
           Cette somme est obtenue en supprimant les termes de la suite harmonique contenant la séquence :  5 , 0 , 0.

            1) pour 5001 on affiche uniquement la valeur approchée avec 20 chiffres significatifs.

            2) On prolonge la somme jusqu'à 1000001.

Remarquez qu'avec la somme, le nombre de termes conservés est toujours affiché.

 

 

             Dénombrons avec le programme B, un peu plus rapide, les termes d'une somme de Kempner pour de grandes valeurs de N.

 

 

 

 

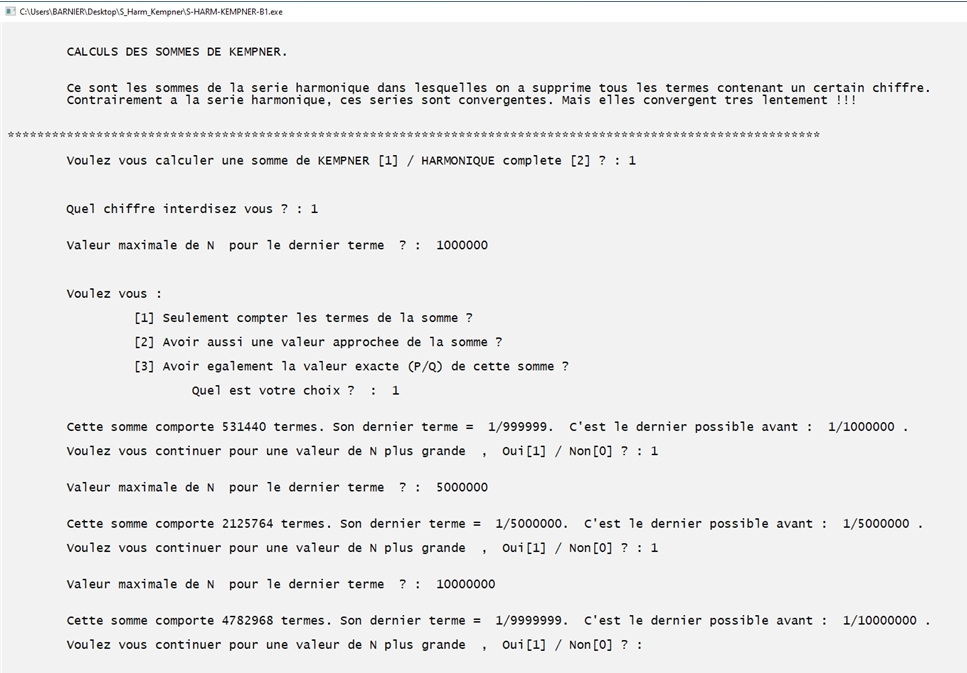
Ce programme permet de :

3)   Déterminer si une fraction P/Q et une somme harmonique.

Si cette fraction est une somme harmonique H(N), le programme la détermine : il donne la valeur de N. Il aura auparavant simplifié la fraction P/Q quand c’est possible.

On peut également choisir un des cas : « normales » , « paires » , « impaires ». Le cas voulu est à indiquer avant le calcul.

Si cette fraction n'est pas une somme harmonique le programme indique la somme qui lui est immédiatement inférieure selon le cas choisi.

Pour cette partie du programme également les sommes H(N) sont determinées de proche en proche.

Il donne la valeur de N et celle de cette somme H(N) sous la forme d'une fraction irréductible. Il précise également le nombre de termes de la suite et le complément qu'il faut rajouter à H(N) pour obtenir la fraction P/Q, sous forme d'une fraction irréductible.

Dans tous les cas ce complément est inférieur au premier terme suivant celui de la somme harmonique indiquée.

Avec la partie  5  du programme qui  utilise  la formule  d'EULER-MASCHERONI, on obtient trés rapidement les 2 valeurs de N consécutives telles que les sommes H(N) correspondantes encadrent un nombre réel H quelconque et ce pour de grandes valeurs de H(N)..

 

Exemples d'utilisations.

 

             1)  Vérifions que la fraction   7129/2520  est bien une somme harmonique.

             2)  Puis que la fraction  761/560  est bien une somme harmonique paire.

 

 

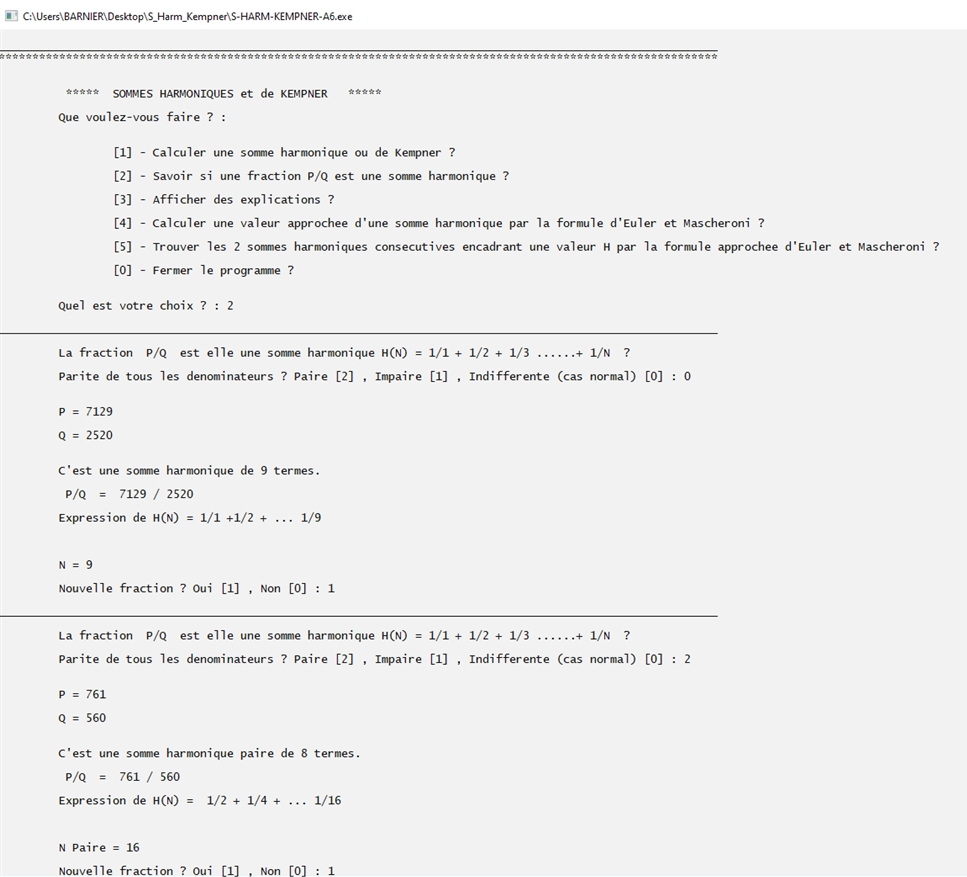
             3)   412/290  n'est pas une somme harmonique, elle vaut :  H(1)  +  61/145.

            4)   412/190  non plus. Elle vaut  :  H(4)  +  97/1140.

 

             5)   167/377 ne peut-être une somme harmonique (impaire) car elle est plus petite que 1.

             6)   167/63  n'est pas une somme harmonique impaire, le programme donne la somme impaire immédiatement inférieure et l'appoint sous forme fractionnaire.

 

 

 

 

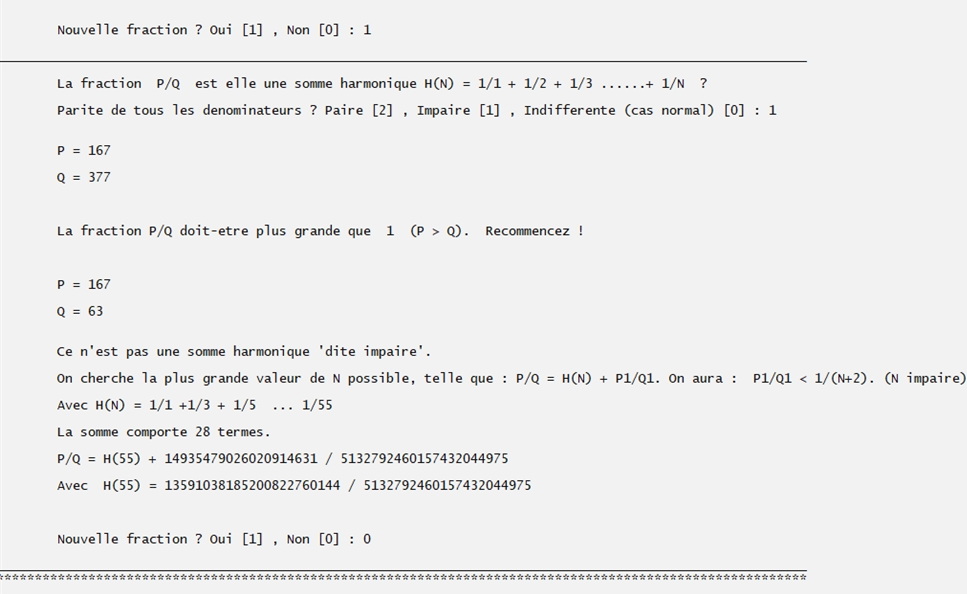
Ce programme permet de :

4)   Déterminer rapidement une valeur approchée d'une somme harmonique de dernier terme N.

L'utilisation de la formule d'EULER-MASCHERONI et de la constante du même nom comportant un grand nombre de décimales, ainsi que du développement asymptotique de cette formule avec un ordre suffisant, permettent d'obtenir trés rapidement la valeur de la somme H(N) pour N trés grands avec une trés bonne précision. Cette formule évite un calcul termes à termes de la somme.

Aprés l'introduction de la valeur de N, le programme indique la précision maximum possible sur le résultat (voir (****) pour les explications). Les paramètres des calculs internes sont alors automatiquement determinés pour assurer cette précision.  On peut alors choisir le nombre de chiffres du résultat.   

La valeur de H(N) est alors affichée. Le calcul ne dure que quelques secondes. Par exemple pour atteindre une somme voisinant 100,  N doit-être voisin  de 10^43. Le programme dans sa partie  1  devrait mettre un temps infini pour trouver ce résultat (en sommant termes à termes, voir remarque  (**) ), alors qu'ici dans la partie  4  il ne met que quelques secondes.

La précision maximum possible sur H(N) croit  avec N. Elle est plafonnée par le nombre de décimales utilisé pour la constante d'EULER-MASCHERONI (170 000).

Des calculs théoriques concernant la précision maximum possible sont en cours. Pour le moment celle-ci est donnée à titre indicatif mais les vérifications sur des exemples sont concluantes.

 

Exemples d'utilisations.

             Calcul de la valeur approchée de la somme Harmonique pour N = 1 000 000 avec 182 décimales en se servant de la formule d'Euler Mascheroni.

 

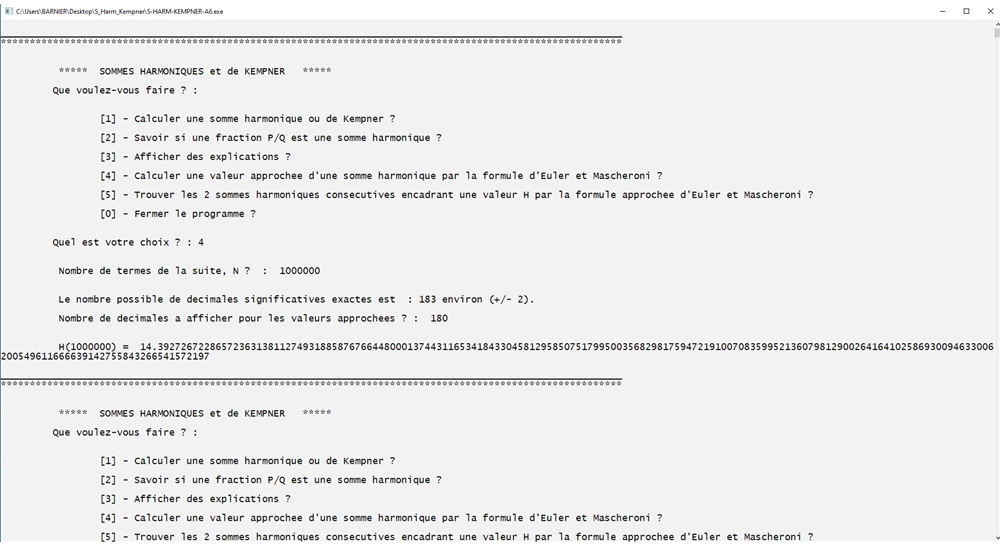
             Vérification du résultat par le calcul termes à termes de la  même somme avec la partie 1 du programme et le même nombre de chiffres significatifs.

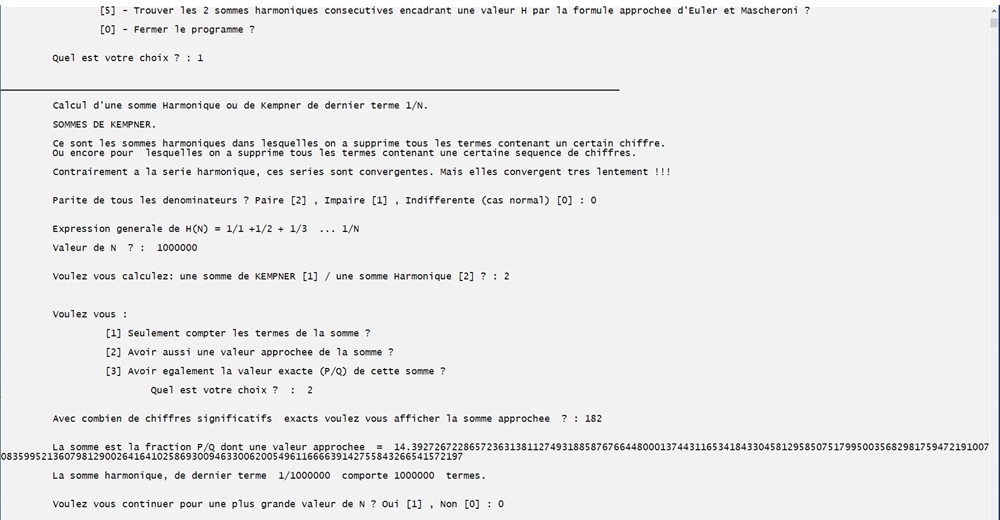
Les 2 sommes sont identiques.

 

 

             Calcul de la somme pour  N = 1 000 000 000 000 avec la formule d'Euler Mascheroni et 50 décimales.

             Puis pour N = 1 000 000 000 000 000 000 dans les mêmes conditions.

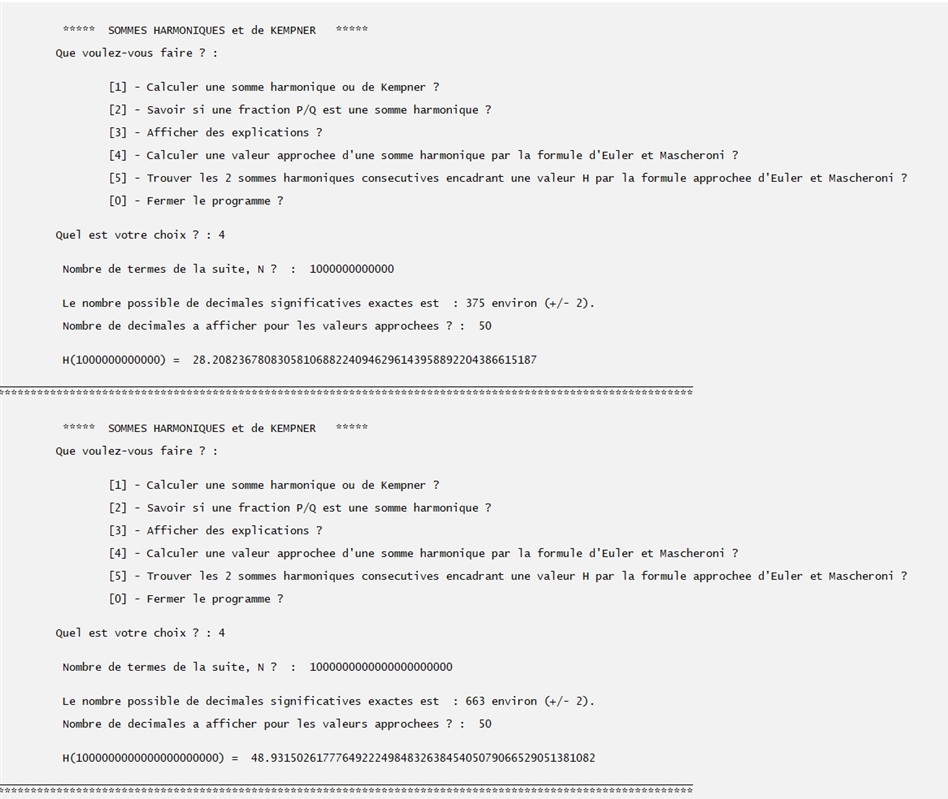
[ Il reste à prouver ou à infirmer la validité des approximations du programme pour ces grandes valeurs de N. ]

 

 

 

Ce programme permet de :

5)  Trouver rapidement les 2 valeurs consécutives de N telles que les sommes harmoniques correspondantes encadrent un nombre réel H quelconque.

Toujours en utilisant la formule d'EULER-MASCHERONI et par approximations successives, on détermine trés rapidement les 2 valeurs consécutives de N dont les sommes correspondantes encadrent un nombre H réel quelconque.

La encore après avoir demandé  la valeur du réel H et avant d'afficher les résultats, le programme indique la précision maximum possible pour le calcul des sommes H(N). Ceci compte tenu de la valeur de N (entière) qu'il a trouvé. On peut alors choisir librement le nombre de chiffres cette l'affichage.

On obtient les 2 valeurs de N et les sommes H(N) correspondantes, ainsi qu'une approximation de N (en puissances de 10).

Le programme est limité par le nombre de décimales utilisé pour la constante d'EULER-MASCHERONI (170 000). Il indique que cette limite est dépassée quand c'est le cas.

Pour H = 1000 (N à 435 chiffres), le calcul est trés rapide. Pour H = 10 000 (N à 4343 chiffres), il est de moins d'une mn. Pour H = 100 000, il mettra plus de 10 mn. Pour H = 1000 000, les capacités du programme sont dépassées.

Là encore, des calculs théoriques concernant la précision maximum possible sont en cours. Pour le moment celle-ci est donnée à titre indicatif mais les vérifications sur des exemples sont concluantes.

 

Exemples d'utilisations.

 

             On trouve successivement les sommes harmoniques consécutives qui encadrent les valeurs  : 50  puis  200 et  enfin  500.

 

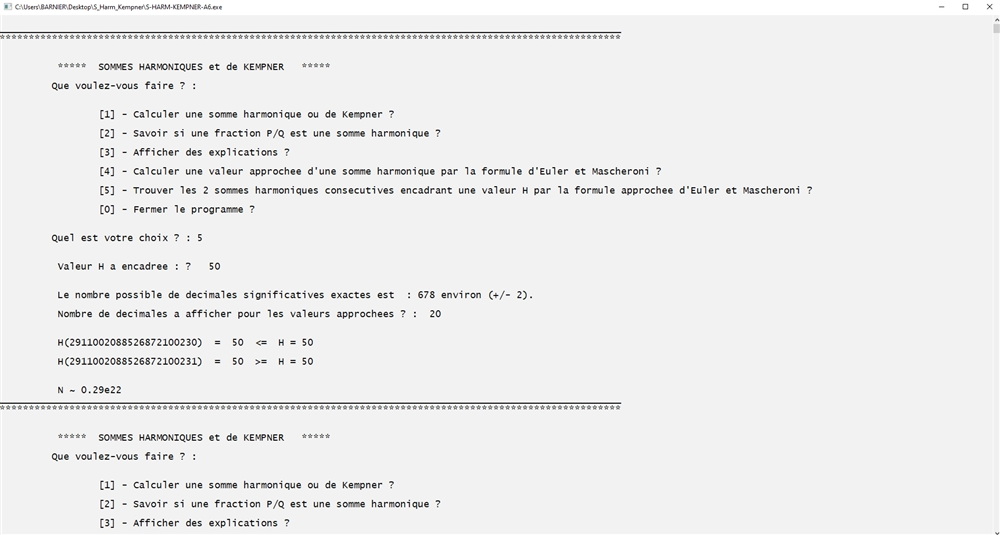
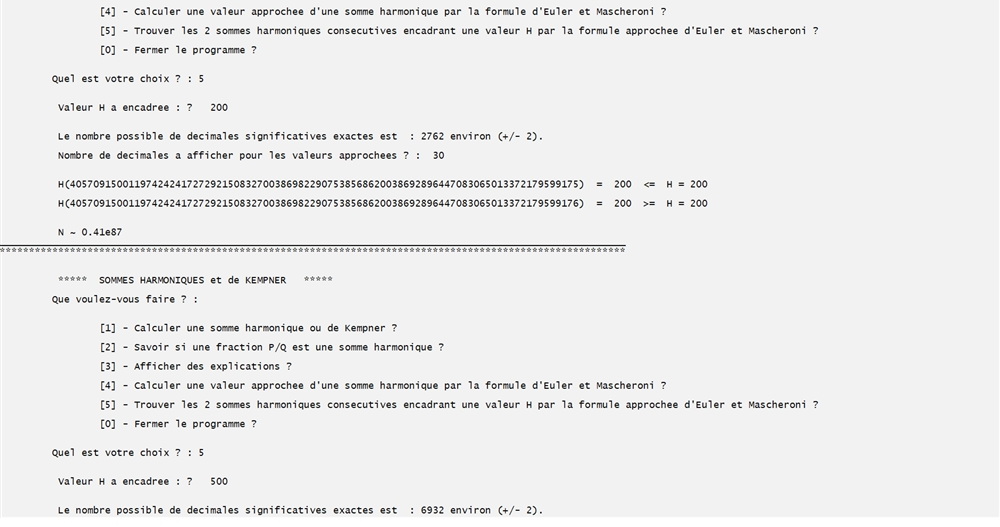
             On refait le dernier calcul avec plus de décimales pour se rendre compte de l'encadrement :

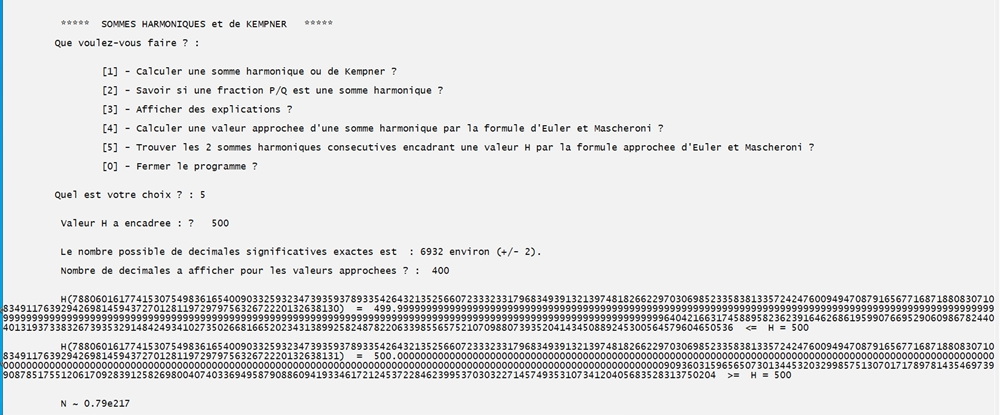
[Ici aussi, Il reste à prouver ou à infirmer la validité des approximations du programme pour les grandes valeurs de N. ]

 

 

 

 

Ce programme existe en 2 versions :

 

La version A  permet de calculer les sommes Harmoniques complètes et celles de Kempner, dans tous les cas pour ces dernières (1 seul chiffre interdit, ou une séquence de chiffre interdite). On peut aussi choisir entre "sommes paires",  "sommes impaires" et "sommes complètes".  Pour ses calculs, cle programme liste toutes les valeurs possibles de 1 à N des dénominateurs en testant chaque valeur pour éliminer celles à rejeter. Son algorithme est un peu moins rapide que celui de la version B.

Cette version A propose également le calculs trés rapide et précis de H(N) connaissant N ainsi que la determination précise de N connaissant H(N) par l'utilisation de la formule ou développement d'EULER-MASCHERONI.

 

La version B permet de calculer les sommes Harmoniques complètes et celles de Kempner, mais pour ces dernières, uniquement  dans les cas ou un seul chiffre est interdit. Cette version utilise un algorithme plus rapide. Cel dernier ne calcule que les dénominateurs contenant les 9 chiffres autorisés. Cette version ne possède pas les options "Sommes Paires" et "Sommes Impaires" et ne permet pas non plus de déterminer si une fraction est une somme Harmonique.

L'extension NTL du C++ utilisée ici permet de calculer avec des entiers de tailles  quelconques (ZZ) et des réels de tailles quelconques également (RR). Les limites réelles viennent des temps de calcul tributaires des processeurs et de la capacité en mémoire vive des ordinateurs.

Dans ces 2 versions la saisie des données est sécurisée : une entrée incompatible est re-demandée et ne provoque pas un "plantage".

 

 

 

(*) Le résultat est vérifiable facilement  pour les suites de Kempner dans lesquelles on supprime les termes contenant un chiffre. Les nombres de termes inférieurs ou égaux à 10 n sont  :

Dans le cas plus général d’une séquence de chiffres interdite, le comptage manuel est plus délicat. Mais on peut vérifier  les résultats du programme (A) sur des cas particuliers.

On constate que le pourcentage de termes que l’on garde par rapport à la suite harmonique complète tend vers zero quand n augmente.

Par exemple dans le dernier cas ce pourcentage varie comme 9 n/ 10 n  =  (0.9) n

 

 

 

(**) Deux points de vue sur la vitesse de croissance vers l'infini de la suite harmonique :

 

Première réflexion : (Alain Barnier)

 

La série harmonique diverge en tendant extrèmement lentement vers l'infini. La démonstration de sa divergence est classique.

Pour se rendre compte de cette lenteur, calculons à l'aide de notre programme les sommes harmoniques H(N) avec 11 chiffres significatifs pour des puissances de 10 consécutives de N :

 

Pour N = 10^7    on a H(N) = 16.695311366

Pour N = 10^8    on a H(N) = 18.997896414

Pour N = 10^9    on a H(N) = 21.300481502

Pour N = 10^10  on a H(N) = 23.603066595

Pour N = 10^11  on a H(N) = 25.905651688    Pour ce dernier calcul un ordinateur assez puissant a mis plus de 30 heures.

Mais ces valeurs approchées peuvent-être obtenues trés rapidement dans la partie 4 qui utilise la formule d'EULER-MASCHERONI

 

Les accroissements successifs des sommes sont (avec 10 chiffres significarifs):

 

2.302585048

2.302585088

2.302585093

2.302585093

 

Nous voyons qu'ils ont l'air de croitre et de tendre vers une limite.

 

On peut prouver assez facilement la propriété (voir ci après) : si  N > n  en posant : A(n,N) = H(N) - H(n) = 1/(n+1) + 1/(n+2) + ... + 1/(N-1) + 1/N

alors quand n et N tendent vers l'infini   [ ln(N/n) - A(n,N) ]  tend vers zéro.

 

En particulier si n = 10^t et N = 10^(t+1) avec t entier positif, on a ln(N/n) = ln (10^(t+1)/10^t )= ln(10).

Donc quand  t  tend vers l'infini, n et N tendent aussi vers l'infini et A( 10^( t+1) , 10^t ) tend vers ln(10) = 2.302585093  (10 chiffres significatifs).

 

Autrement dit, l'accroissement de la somme harmonique quand  les valeurs des derniers termes sont des puissances de 10 consécutives, tend vers ln (10) quand ces puissances consécutives augmentent indéfiniment.  

 

 

Nous voyons sur les résultats ci dessus que la différence des sommes harmoniques pour des puissances consécutives de 10 se "stabilise" assez rapidement vers 2.3 quand on ne garde que 2 chiffres significatifs.

Pour avoir une somme H(N) d'environ 26 il fallait N = 10^11.

Quand on augmente de 1 l'exposant de la puissance de 10 représentant N, la somme H(N) augmente de 2.3 (à l'approximation près).

Pour atteindre une somme de 100 , il faudra augmenter l'exposant 11 de (100 - 26)/(2.3) = 32 environ.

Pour calculer H(N) pour N = 11 + 32 = 43 il faudra trés grosso-modo 10^32 fois plus de temps que pour 10^11 puique le nombre de termes de la suite aura été multiplié par 10^32.

Il faudra donc environ (30 heures) x (10^32) = 3 x 10^33 heures.

Comme 1 siècle vaut : 24 x 365 x 100 = 876000 heures, il faudra avec le même ordinateur : (3 x 10^33)/876000 = (3000000/876000) x 10^27 siécles = 3.4 x 10^27 siècles soit 3.4 milliards de milliards de milliards de siècles environ.

On peut déterminer exactement et rapidement ces valeurs de N en utilisant la formule d'EULER-MASCHERONI . C'est l'objet de la partie  5 du programme. On peut avec la même formule trouver de trés bonnes approximations de H(N) pour de trés grandes valeurs de N.

 

Démonstration de la propriété :

 

Nous savons que ln x = valeur de l'intégrale définie de 1 à x de la fonction 1/x.

 

Donc si N > n , ln(N/n) = ln(N) - ln(n) = valeur de l'intégrale définie de  n  à  N  de la fonction 1/x.

 

Donc ln(N/n) est l'aire sous la courbe de la fonction 1/x entre les valeurs n et N de x.

 

si n et N sont des entiers et qu'on découpe l'intervalle [n,N] toutes les unités, on voit que :

On a donc l'encadrement :

 

A(n,N) < ln (N/n) < A(n,N) + 1/n - 1/N

 

soit encore :

 

0 < ln(N/n) - A(n,N) < 1/n - 1/N

 

Comme (1/n - 1/N) tend vers zéro si n et N tendent vers l'infini tous les deux, alors dans les mêmes conditions la différence de ln(N/n) et de A(n,N) tend aussi vers zéro.

 

Si  N/n  tend vers une valeur k ou est égal à une valeur k, alors l'accroissement A(n,N) tend vers ln(k) quand n et N tendent tous les deux vers l'infini.

 

Remarquons également qu'en posant n = 1 dans la démonstration précèdente on a :

A(n,N) = A(1,N) = H(N) - 1

alors l'inégalité A(n,N) < ln(N/n) < A(n,N) + 1/n - 1/N , s'écrit :

H(N) - 1 > ln(N/1) < H(N) - 1 + 1/1 - 1/N , soit encore :

H(N) - 1 <  ln(N)  < H(N) - 1/N   ou   -1 <  ln(N) - H(N)  < -1/N   ou encore    1 >  H(N) - ln(N)  > 1/N

Soit encore :  1 + ln(N) >  H(N)  > 1/N + ln(N)

 

Finalement :

 

ln(N) + 1/N < H(N) < ln(N) +1

 

La valeur de la somme Harmonique de dernier terme N est comprise entre  ln(N) + 1/N  et  ln(N) + 1.

 

pour N = 10^11 on peut vérifier :   ln(10^11) + 1/(10^11) <  25.905651688 < ln(10^11) +1

11 x 2.302585093 + 1/ (100 000 000 000) <  25.905651688  < 11 x 2.302585093 +1

 

25,328436023 <   25.905651688   < 26,328436023

 

Comme on le présentait, les sommes harmoniques est la fonction log sont liées

 

Pour avoir H(N) valant au minimum 100 : ln(N) + 1/N < 100 < ln(N) + 1

soit  : 1/N -100 <  -ln(N)  <  1 -100   ou  100 - 1/N   >  ln(N)   >  99

99 + 1/N   < ln(N) + 1/N  <  100

99 < ln(N) < 100 - 1/N  (<100)

on doit donc avoir  e^99 < N < e^100

soit : 9,88 x 10^42 < N <  2,69 x 10^43 , ce qui correspond à peu près à notre précèdent calcul.

 

Grosso modo, quand  H passe de 10^t à 10^(t+1) la valeur du nombre de décimale de N est multiplée par 10.

 

 

Deuxième réflexion : (Gérard Lopez)

 

Patience et longueur de temps

Pour se faire une idée de l’extrême lenteur (le mot est faible) de la croissance de la SH, nous avons imaginé un programme de calcul qui additionnerait chaque seconde depuis l’instant zéro du Big Bang les inverses des entiers consécutifs à compter de 1 en donnant la valeur du nombre harmonique correspondant.

Rappelons que, d’après les astrophysiciens, le Big Bang aurait eu lieu il y a environ 13,5 milliards d’années, soit en secondes

     13,5 x 109 x 365 x 24 x 3600 = 425 736 000 000 000 000 ≈ 4,25 x 1017

Nous avons estimé le nombre harmonique correspondant par extrapolation du tableau ci-dessous.

 

Nombre de termes

Valeur du nombre harmonique

Accroissement 10n+1 – 10n

100  = 1

1,000 000 000

 

101  = 10

2,928 968 254

1,928 968 254

102  = 100

5,187 377 518

2,258 409 264

103  = 1 000

7,485 470 861

2,298 093 343

104  = 10 000

9,787 606 036

2,302 135 175

105  = 100 000

12,090 146 13

2,302 254 009

106  = 1 000 000

14,392 726 72

2,302 580 059

107  = 10 000 000

16,695 311 37

2,302 584 65

108  = 100 000 000

18,997 896 41

2,302 585 04

109  = 1 000 000 000

21,300 481 50

2,302 585 09

 

 

 

 

 

 

 

Le compteur,pour plus de 425 mille billions de termes ou encore pour 0,425 trillions de termes,  serait très approximativement aux environs de 40.

Petit calcul proposé aux amateurs : Calculer le temps nécessaire au compteur pour qu’il affiche 2022 dans la partie entière …

C’est encore loin l’infini ?

Il nous semble correct d’ajouter les remarques suivantes :

- D’une part, 1017 est sans doute impressionnant pour beaucoup, mais les mathématiciens en ont vu d’autres et les ordinateurs des informaticiens encore  bien plus. Par exemple,  on a calculé (par un programme, évidemment) le nombre exact de termes nécessaire pour obtenir le premier nombre harmonique qui affiche 100 dans la partie entière :

      Partie entière de Hx = 100  pour la 1ère fois

      si : x = 15 092 688 622 113 788 323 693 563 264 538 101 449 859 497,

      soit x ≈ 1,509 x 1043

- D’autre part, certains estimeraient que la seconde est une unité trop grande concernant la vitesse de calcul des ordinateurs. En effet, les ordinateurs les plus performants, les superordinateurs, brassent des millions de milliards d’opérations par seconde (dans les locaux du CEA, ATOS, le plus puissant des supercalculateurs français atteint 22 pétaflops, soit 22 x 1015 opérations par seconde). On peut donc abaisser l’unité de temps et choisir entre la nanoseconde (1ns = 10 – 9 s), la picoseconde (1ps = 10 – 12 s) et la femtoseconde  (1fs = 10 – 15). Optons pour la plus petite unité (la fs).

  On revient à notre problème et on décide que le compteur ajoute et calcule un nouveau terme 1/n de la série harmonique chaque femtoseconde. Le nombre de termes depuis l’instant zéro du Big Bang s’élève alors à 4,25 x 1017 x 1015  = 4,25 x 1032.

  Dans ce cas, le compteur n’afficherait pas loin de 55/56, mais encore loin de 100.

 Pourquoi l’accroissement du nombre harmonique se stabilise rapidement à compter de 104 à 2,302 ?

On sait que la progression de la série harmonique et son comportement très proches de ceux du logarithme népérien ont amené Leonhard EULER  en 1735 et le mathématicien italien Lorenzo MASCHERONI à proposer la relation suivante :

 

(***) Une remarque sur les sommes harmoniques concernant les fractions égyptiennes (celles de type 2) :

Dans le cas d’une suite « normale » de dernier terme N (en comprenant N), on s'aperçoit facilement que cette somme est le développement égyptien d'ordre N de valeur maximale. Le premier terme étant 1/1 et les suivants prenants chacun leur valeur maximale  :  1/2 , 1/3 , 1/4 , … , 1/N .

La somme harmonique H(N) a donc la valeur maximale que peut prendre un développement égyptien d'ordre N dont le premier terme peut être égal à l'unité. Ce qui veut dire aussi qu'il n'existe pas de développement égyptien d'ordre N pour des fractions supérieures à H(N).

On peut facilement étendre ce raisonnement à des développements égyptiens dont le premier terme est différent de 1/1. On peut aussi l'étendre à des développements égyptiens « pairs » ou « impairs ». Cela permet d'obtenir des majorants pour les fractions dont on cherche des développements égyptiens « pairs » ou « impairs » d'ordres respectifs, N/2 et (N +1)/2.

Par exemples :

 

Pour cette valeur maximale il y a qu'un développement égyptiens possible : la suite harmonique. Pour des valeurs supérieures il y en a aucun. Et pour des valeurs P/Q inférieures le nombre de solutions semble avoir tendance (« statistiquement ») à croître rapidement quand la valeur de la fraction P/Q diminue. Voir plus haut haut, au niveau du premier logiciel, la réflexion à ce sujet.

 

 

(****) Formule d'EULER-MASCHERONI.

 

Elle donne un développement asymptotique de la série Harmonique :

 

 

La voici poussée jusqu'à la puissance 10 de n :

 

 

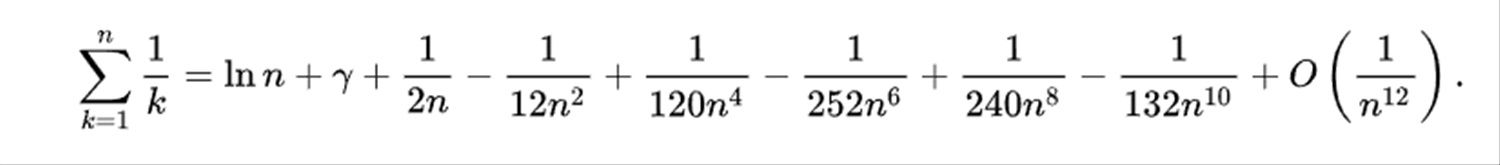
       Gamma est la constante d'EULER-MASCHERONI dont on connait un trés grand nombre de décimales.

 

     

    La formule utilise les nombres de Bernouilli. Voici une manière de les calculer de proche en proche :

     

 

     Ci-dessous la liste des 32 premiers. Ceux de rangs impairs sont nuls. Ceux de rangs pairs sont alternativement positifs et négatifs :

 

 

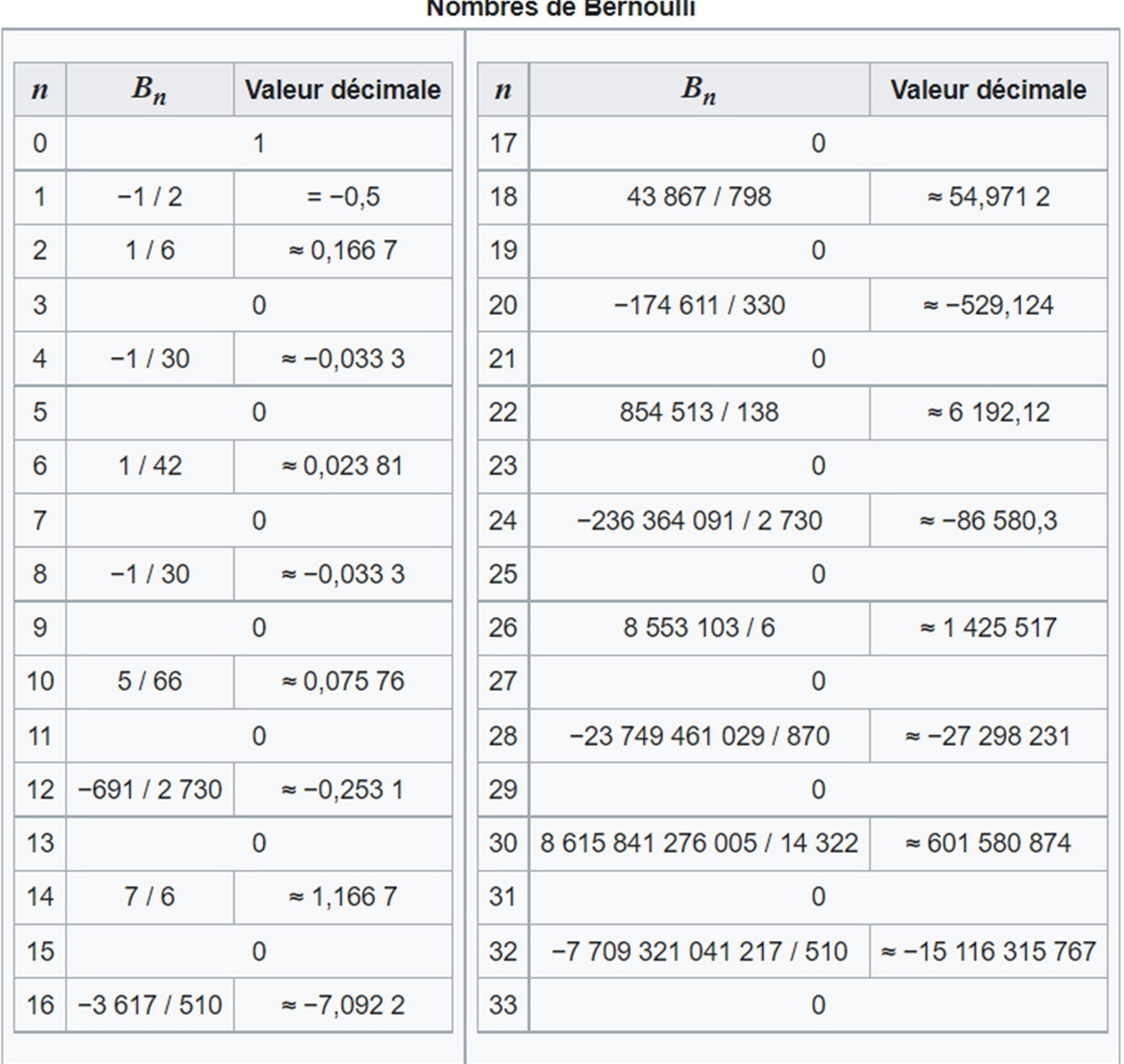
    La série des termes du développement asymptotique est  convergente et alternée quelque soit n. Du moins au début les termes ont une valeur absolue décroissante qui semble tendre vers zéro.

    Dans le programme on utilise les termes du développement asymptotique jusqu'à une puissance maximum  égale à  32 de n. La constante Gamma est utilisée avec 170 000 décimales au maximum. On tente de majorer dans chaque cas le reste négligé du développement asymptotique par la valeur absolue du premier terme négligé. Pour celà, on applique peut-être à tort le théorème de la majoration du reste d'une série alternée décroissante convergente pour justifier cette majoration.

    Les vérifications numériques faites pour certaines valeurs de n avec un grand nombre de décimales pour H(n) semblent confirmer nos majorations. Mais les calculs théoriques n'ont pas été faits et une première approche la mettrais plutôt en doute (Les nombres de Bernouilli devenant trés grands quand l'exposant de n croit.).

   Les calculs utilisent dans chaque cas le nombre de décimales de gamma et le nombre de termes du développemen justes nécessaires (moyennant notre majoration),  pour avoir la précision souhaitée.

   Les limites du programme en précision des résultats et grandeurs des données possibles semblent dépendre de ces 2 paramètres.

 

 

 

  < = >  

 Téléchargement d'un setup d'installation du programme pour Windows :

Solution recommandée, la plus pratique.

https://alainb-sites.fr/programmes/setup_S_Harmoniques.zip

 

 

 

 

 Code commenté des programmes au format RTF

 

[A venir]

  

 

 

[A venir]

 

@ @ @

 

  Liens sur le sujet  

 

 

 

Ci-dessous 2 liens vers des sites consacrés aux suites de Kempner et à des sujets annexes. Ces pages renvoient aussi à d'autres concernants ce sujet. On y trouve la démonstration de la convergence de ces suites.