Sommes des diviseurs d'un nombre
Nombres presque parfaits et nombres parfaits
a b c d e f g h I j k
Programme permettant d'afficher ou dénombrer toutes les sommes de diviseurs d'un nombre N (sauf lui-même) égales à ce nombre ou à un autre nombre S fixé au début du calcul.
Table des matières :
Reflexions sur la somme des diviseurs d'un nombre et formule permettant de la calculer rapidement.
- 1 - Listing des valeurs de N avec leurs nombres de diviseurs et de solutions.
- 2 - Recherche de cas particuliers : N Parfaits - N Abondants avec 0 solution.
- 3 - Tri des valeurs de N selon la parité de la somme des diviseurs.
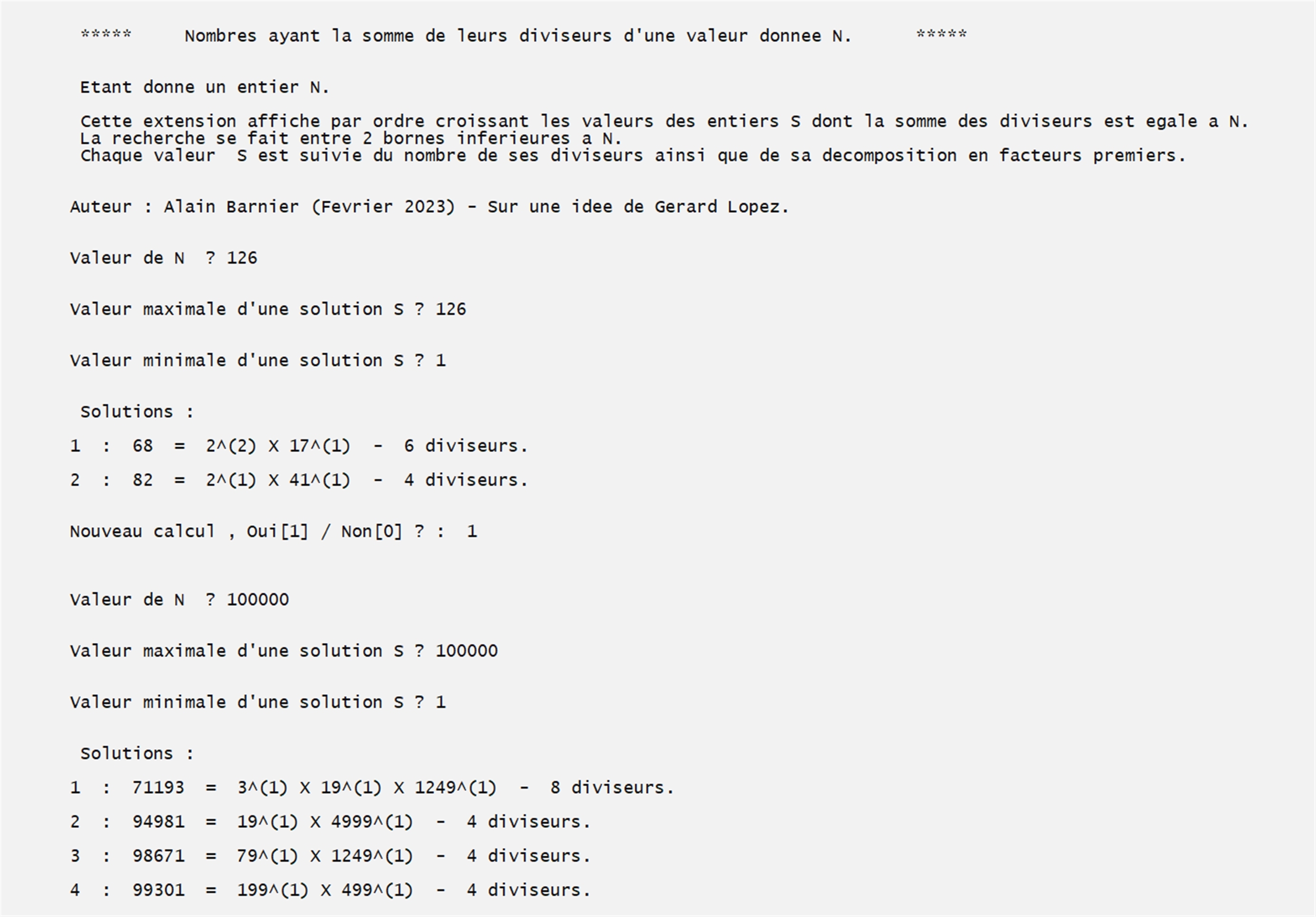
- 4 - Trouver tous les entiers dont la somme des diviseurs a une valeur donnée.
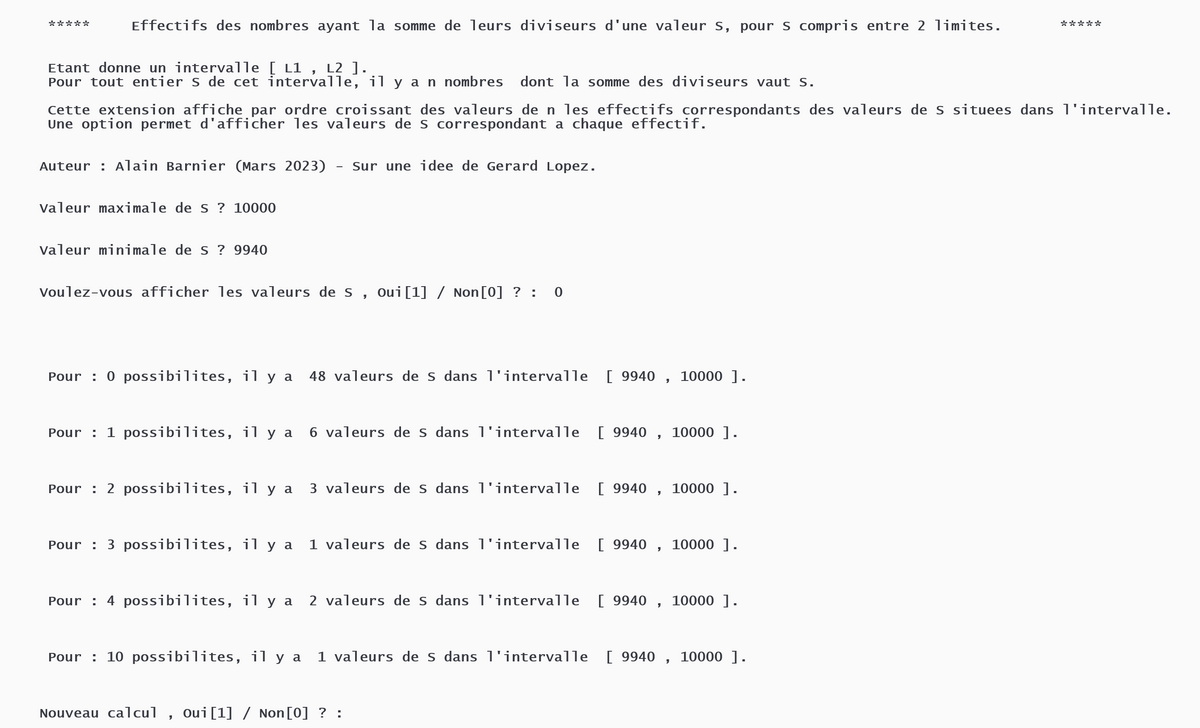
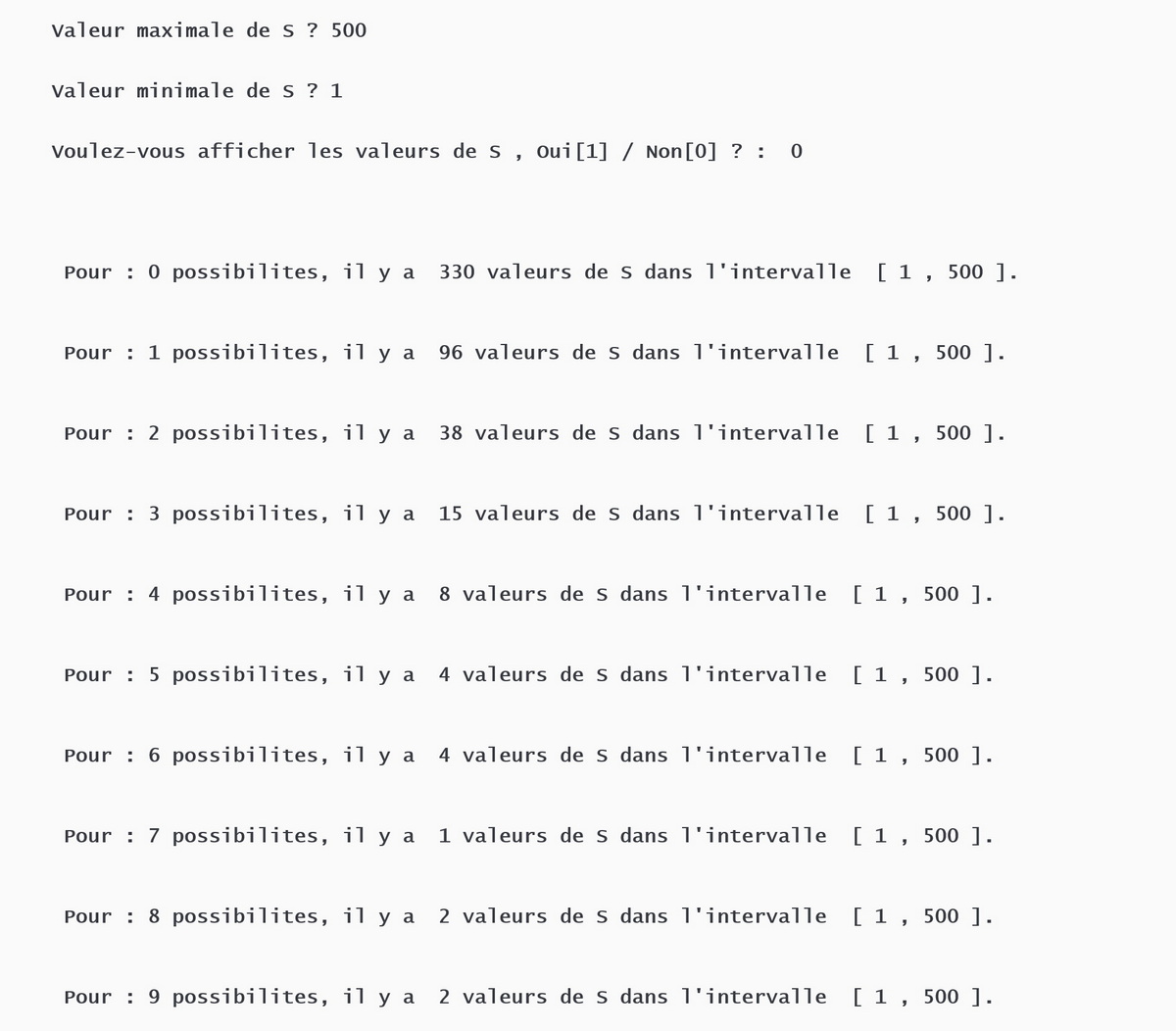
- 5 - Effectifs des nombres ayant la somme de leurs diviseurs d'une valeur S, pour S compris entre 2 limites.
Vocabulaire courant
· Diviseurs propres d’un nombre : ce sont tous ses diviseurs à l’exception de lui-même.
· Nombres parfaits : Les nombres qui sont égaux à la somme de leurs diviseurs propres.
· Nombres presque parfaits ou semi-parfaits : Nombres égaux à une ou des sommes composées d’une partie de leurs diviseurs propres.
· Nombres abondants : La somme de leurs diviseurs propres leur est supérieure. Ils peuvent être presque parfaits.
· Nombres déficients : La somme de leurs diviseurs propres leur est inférieure. Ils ne sont donc ni parfaits, ni presque parfaits.
Il y a d'autres catégories de nombres liées à leurs diviseurs.
Les propriétés de ces nombres ont été étudiées très tôt par les mathématiciens.
Citons entre autres :
· La formule d'Euclide.
· Il y a peu de nombres parfaits. 49 sont connus.
· Y a-t-il une infinité de nombres parfaits ? On pense que oui.
· Une conjecture : Il n'existe pas de nombres parfaits impairs.
Voir les liens proposés ci-dessous pour de plus amples détails sur les recherches.
Voici comment procède le programme :
Soit N un entier, le programme commence par chercher tous ses diviseurs.
La solution qui consiste à le diviser par les entiers de 2 à racine carrée de N, devient rapidement très longue quand N grandit.
C'est pourquoi le programme réalise la décomposition en facteurs premiers de ce nombre.
Soit : N = aα × bβ x cγ ... avec : a, b, c premiers.
N a alors (α + 1) x ( β + 1) x (γ + 1) ... diviseurs distincts.
En effet, un diviseur est un produit de la forme : aα1 × bβ1 x cγ1...
ou α1 , β1 , γ1 ... peuvent prendrent des valeurs comprisent entre 0 et α, 0 et b, 0 et g .....
Pour des nombres N, inférieurs à 1014 ou 1015, la décomposition en facteurs premiers est très rapide.
Pour des nombres N supérieurs à ces valeurs, cela dépend de la grandeur des facteurs premiers.
La décomposition faite, les diviseurs sont calculés très rapidement.
Soit D le nombre des diviseurs propres (ce sont tous les diviseurs sauf N lui-même). Le programme doit calculer toutes les sommes de ceux-ci (partielles ou complètes) qui sont égales à N ou à un nombre S fixé au début du calcul.
Il vérifie d'abord :
· Si la somme de tous les diviseurs propres est égale à N. Dans ce cas, le nombre est parfait et il est inutile de continuer.
· Si la somme de tous les diviseurs propres est inférieure à N. dans ce cas, le nombre est déficient et il est inutile de continuer les calculs.
Dans les autres cas il doit examiner tous les cas possibles de sommes partielles de diviseurs de N.
C'est-à-dire toutes les sommes de diviseurs appartenant à un sous-ensemble de ceux-ci.
Comme il y a D diviseurs propres, il y a 2D sous ensembles.
Autre façon de procéder, sans calculer tous les diviseurs du nombre :
Pour tout nombre premier a, les diviseurs de aα sont : 1 , a , a2 , a3 , ...... , aα .
La somme de tout ses diviseurs est donc : (aα+1 - 1)/(a - 1). C'est la somme des termes d'une suite géomètrique.
Si N = aα x bβ x cγ ... avec : a, b, c premiers,
alors, la somme de tous ses diviseurs vaut : (1 + a + a2 + a3 + .. + aα) x (1 + b + b2 + ... + bβ) x (1 + c + c2 + ... + cγ) x ....
Les diviseurs de N étant tous les termes du développement de ces produits.
(D'une façon générale, la somme des diviseurs du produit de 2 ou plusieurs nombres premiers entre eux deux à deux est le produit des sommes de chacun).
Cette somme est donc : (aα+1 - 1)/(a - 1) x (bβ+1 - 1)/(b - 1) x (cγ+1 - 1)/(c - 1) x ...
Une fois déterminer la décomposition en facteurs premiers d'un nombre, on peut donc facilement calculer la somme de tous ses diviseurs sans les calculer tous.
Le programme existe en 2 versions :
La version A - Celle-ci, pour examiner les 2D cas utilise les puissances de 2 consécutives : 2(D + 1) et 2D , en se servant de la représentation binaire de tous les nombres compris entre ces deux valeurs.
Il est un peu plus rapide que la version B.
Pour un nombre de 30 diviseurs, il met environ 45 secondes pour dénombrer toutes les solutions.
La version B - Cette version, pour trouver tous les sous-ensembles de l'ensemble des diviseurs, utilise un algorithme différent et ne se sert pas des nombres compris entre 2(D + 1) et 2D.
Elle est un peu plus lente que la version A, et met environ une minute pour dénombrer les solutions quand il y a 30 diviseurs.
Pour ces deux programmes le nombre de cas à examiner et multiplié par 2 chaque fois que l’effectif des diviseurs augmente de 1. Le temps de recherche et donc également multiplié par 2 environ.
On voit qu'on sera vite limité par ce temps, à moins d'avoir un ordinateur extrêmement puissant.
D'autre part, le programme est écrit en langage C++ 64 bit et n'utilise pas l'extension NTL qui permettrait de travailler avec des entiers de tailles quelconques.
On est donc limité à des entiers inférieurs à 263 - 1.
Le programme A sera donc limité à 61 diviseurs puisqu'il se sert du nombre 2(D + 1).
Le programme B, lui, n'est pas limité par le nombre de diviseurs, mais évidemment par le temps de calcul.
Pour ces 2 versions, la saisie des données est sécurisée : une entrée incompatible est re-demandée et ne provoque pas un "plantage".
Exemples de fonctionnement pour des valeurs simples ou extrêmes :
On verifie que 28 est parfait :
On trouve les 6 solutions pour 80 :
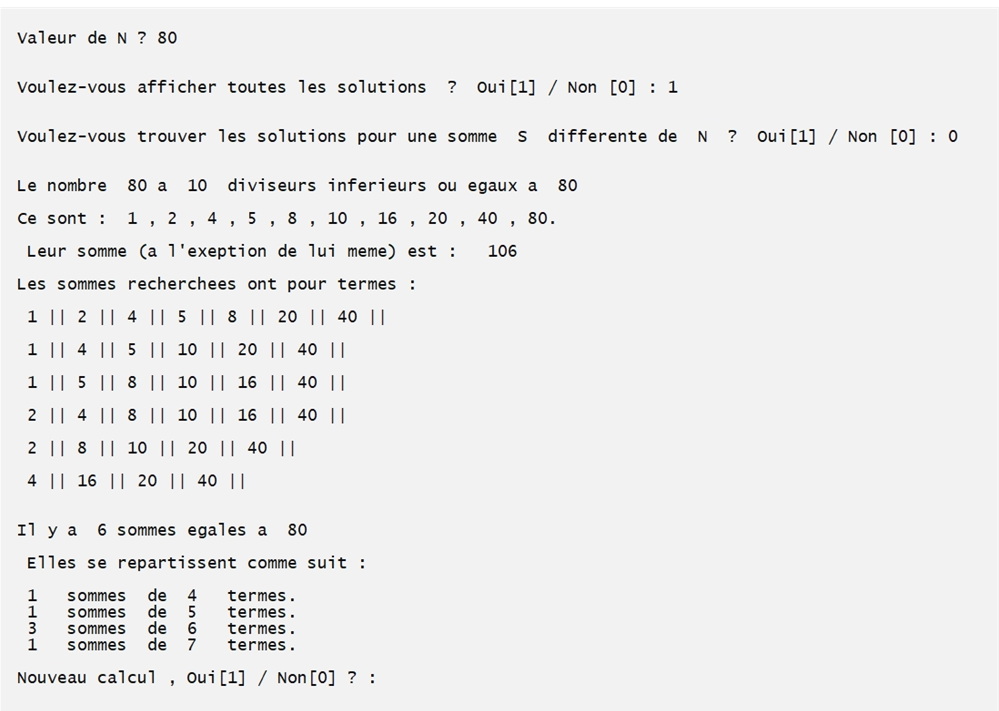
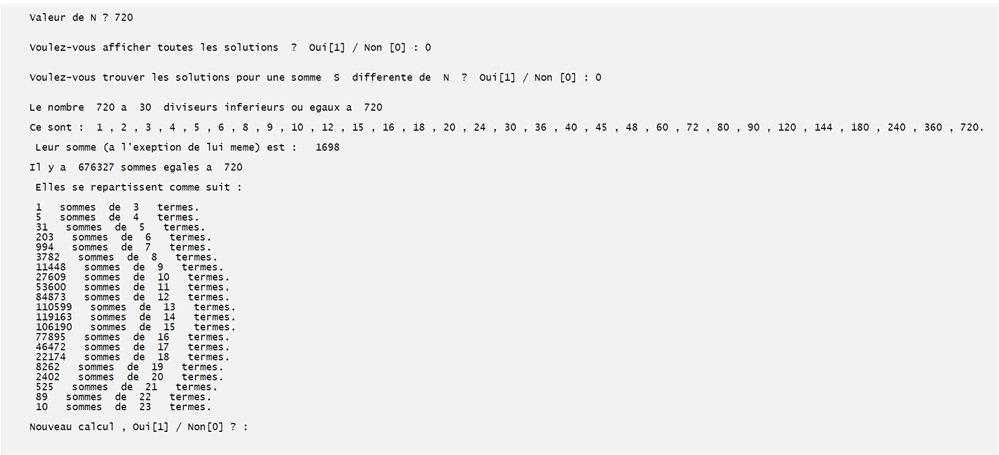
On compte les solutions pour 360 :
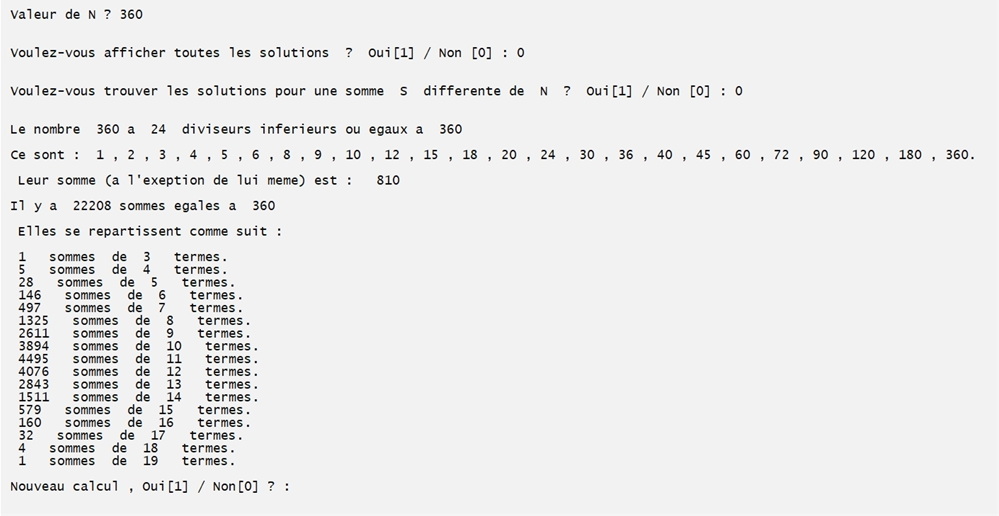
On teste le programme pour N = 263 - 1. Il ne se produit pas d'erreur. Les facteurs premiers étant inférieurs à cette limite et la somme des diviseurs propres également !
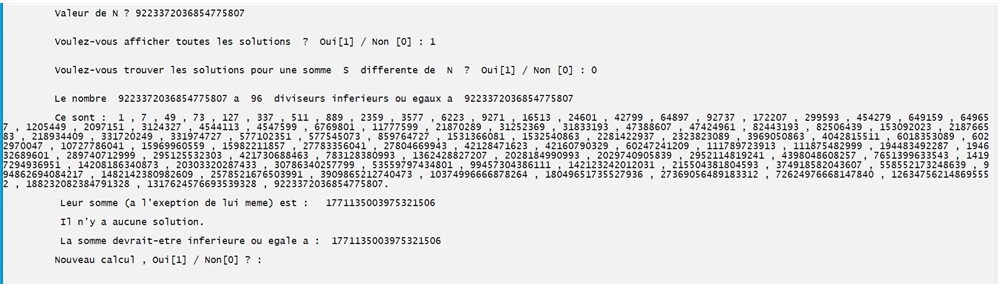
On teste un grand nombre parfait :
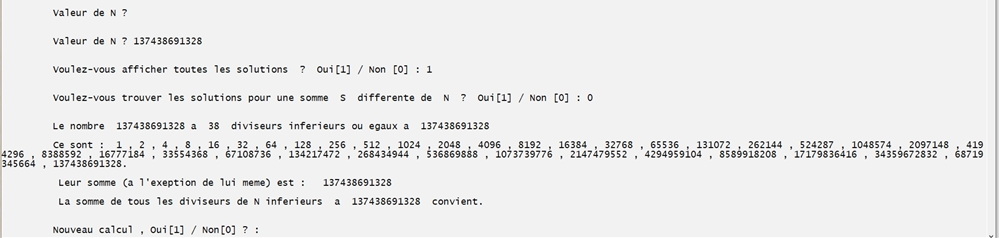
On teste le suivant. beaucoup plus grand !
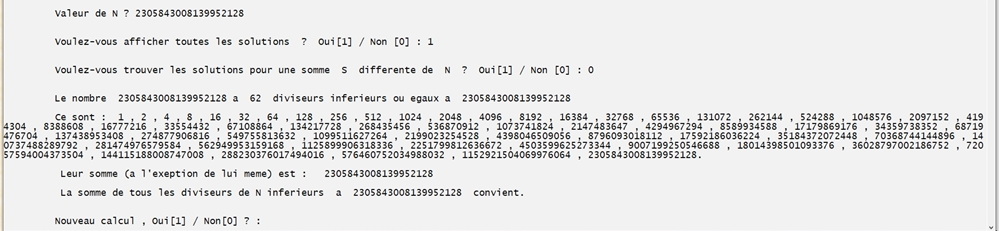
On affiche les solutions pour N = 80, mais pour une somme S = 100, supérieure.
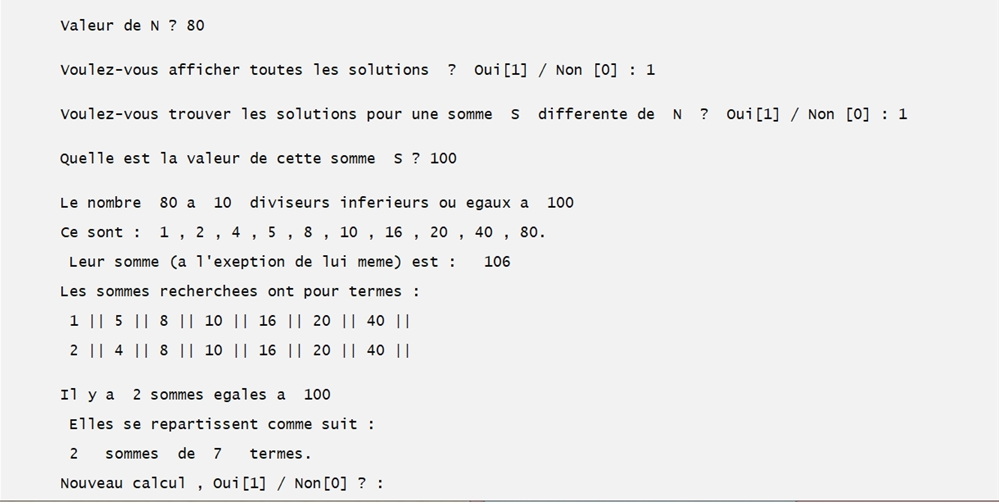
On affiche toutes les solutions pour N = 1230.
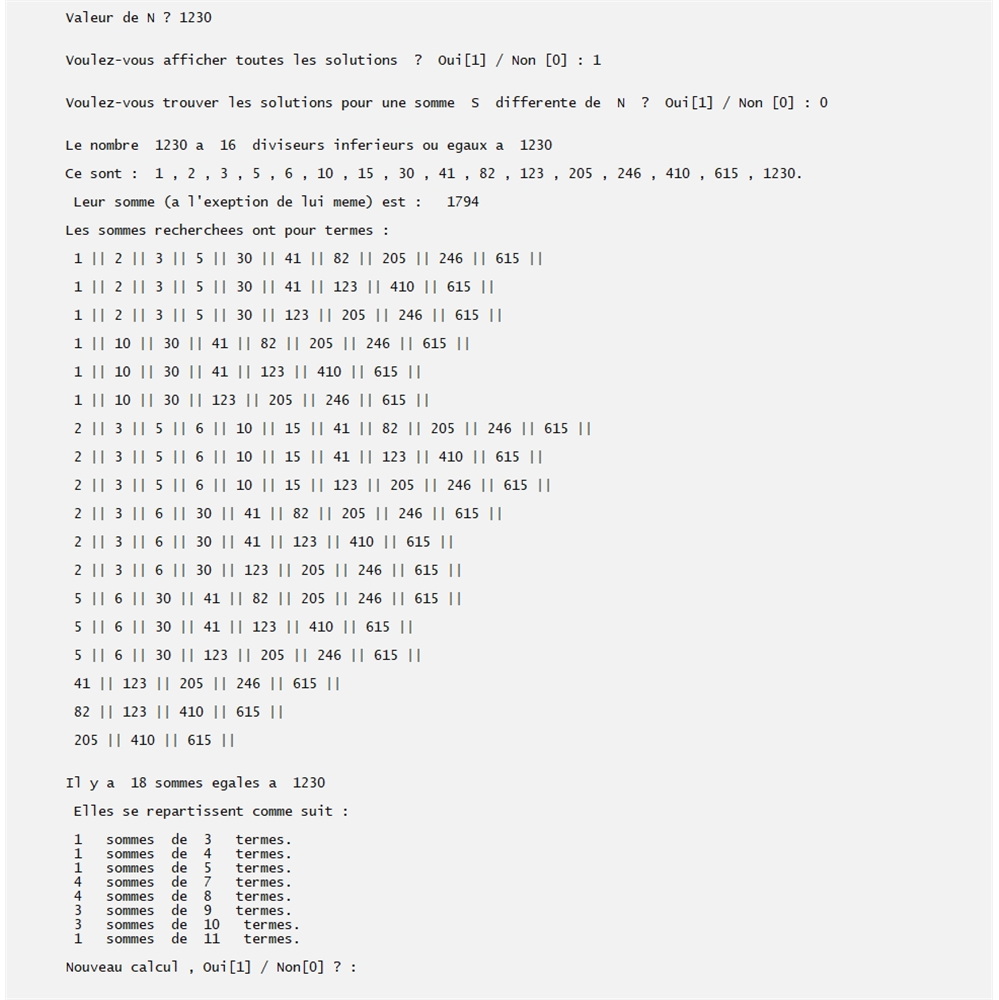
On affiche toutes les solutions pour N = 1230 et pour une somme S = 320, inférieure.
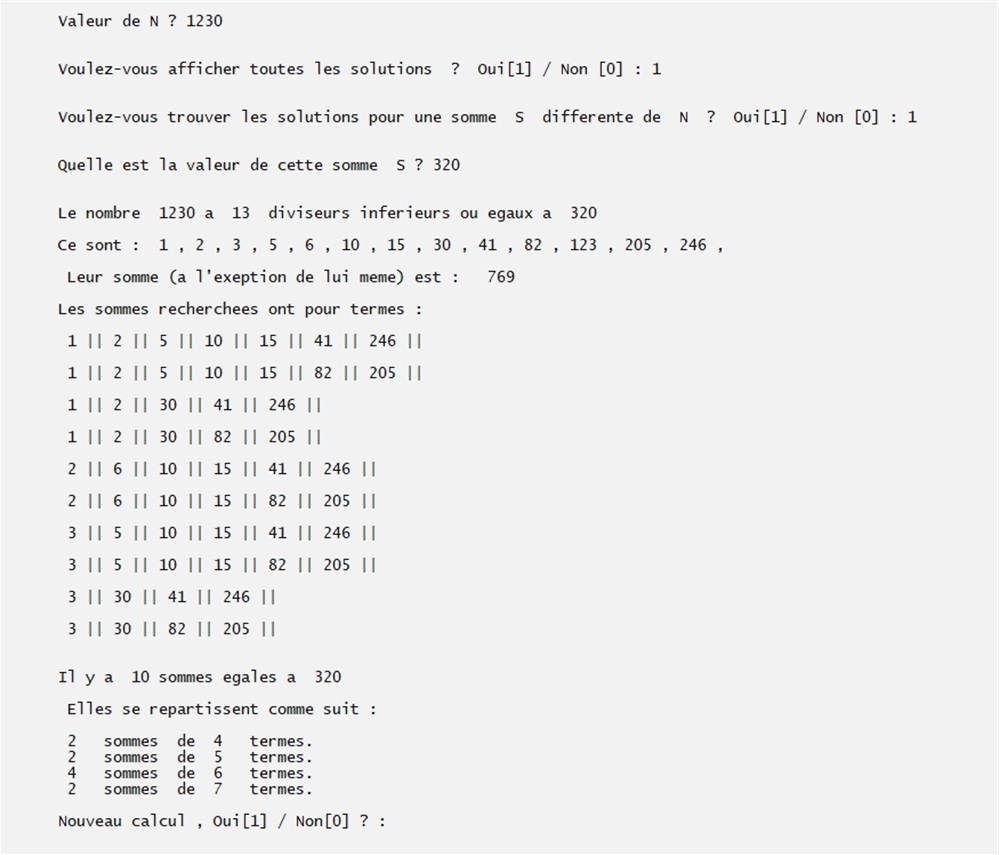
On compte les solutions pour N = 720. Il faut 45 s avec la version A et 1 mn avec la B.
Fonctionement et but des 5 extensions.
Extension 1 : Elle permet d'obtenir un listing des nombres entiers compris entre deux valeurs choisis au début du programme avec au regard de chaque nombre :
- S'il est déficient.
- S'il est parfait.
- Le nombre de sommes de diviseurs propres de ce nombre qui lui sont égales (nombre abondant). Le cas ou il y a "0 somme" est signalé par des astérisques en fin de ligne.
Pour chaque nombe, ces indications sont toujours suivies de l'effectif de ses diviseurs propres ainsi que de leur somme.
Les limites du programme sont celles du programme initial.
Extension 2 : Elle permet de rechercher pour des entiers compris entre deux valeurs choisises, ceux qui :
- Sont parfaits.
- Sont abondants, mais qui ne sont égaux à aucune somme de leurs diviseurs propres (0 solution).
Les nombres abondants sont suivis du nombre de leurs diviseurs propres et de la somme de ceux-ci (qui leur est supérieure).
Les nombres parfaits sont suivis du nombre de leurs diviseur propres.
Une option permet de ne calculer et afficher que les nombres parfaits.
Pour afficher ces résultats, cette extension 2 est plus rapide que la 1. On peut utiliser de grandes valeurs quand on recherche uniquement les nombres parfaits.
Extension 3 : Elle permet d'afficher le listing des valeurs de N, entre 2 limites choisies. Chaque valeur de N étant suivie du nombre de ses diviseurs (y compris N) ainsi que de leur somme. Ces valeurs sont numérotées, celà permet d'en évaluer rapidement l'effectif.
On peut choisir de n'afficher que les valeurs de N pour lesquelles la somme des diviseurs est : paire / impaire / quelconque.
Limites du programme : N doit-être inférieur à 263 - 1. De plus, pour trouver les diviseurs de N, l'algorithme le décompose en facteurs premiers. On est donc limité par la rapidité de la décomposition (à partir de nombre de 14 décimales).
REFLEXIONS et REMARQUES
Recherches de Gérard Lopez :
Deux remarques d'Alain Barnier :
Remarque 1 : Caractérisation d'un nombre entier dont la somme de tous les diviseurs est impaire.
Proposition : Pour que la somme de tous les diviseurs d’un nombre entier N soit impaires, il faut et il suffit, que dans la décomposition en facteurs premiers de ce nombre, les facteurs premiers différents de 2 aient des puissances paires.
Démonstration 1 :
Rappels :
Propriété 1 : pour qu’une somme d’entiers soit impaire, il faut et il suffit que les termes impairs de cette somme aient un effectif impair.
Propriété 2 : pour qu’un produit de nombres entiers soit impair, il faut et il suffit qu’ils soient tous impairs.
La décomposition en facteurs premiers de tout nombre entier N peut s’écrire sous la forme :
N = (2^n) x (p1^k1) x (p2^k2) x (p3^k3) x … (pi^ki)
p1, p2 p3 , … pi étant des nombres premiers tous différents entre eux et tous différents de 2.
n étant un entier positif ou nul (il vaut zéro si le nombre est impair).
k1, k2 k3 …, ki sont des entiers positifs et i un entier positif ou nul (il vaut zéro si N est une puissance de 2 ou est égale à 1).
Les diviseurs de N sont tous les nombres de la forme : (2^t) x (p1^t1) x (p2^t2) x (t3^t3) x … (ti^ti).
Ou t est un entier compris entre 0 et n
t1 un entier compris entre 0 est k1
t2 un entier compris entre 0 est k2
………………………………………
ti un entier compris entre 0 est ki.
Trois cas sont à envisagés :
Dans ce cas, les diviseurs pairs de N, s’i y en a, sont ceux pour lesquels t n’est pas nul.
Tous les autres sont les diviseurs impairs et ils sont de la forme : (p1^t1) x (p2^t2) x ….(pi^ti).
En effet, les nombres premiers p1, p2 … pi sont tous impairs, donc leurs puissances aussi et le produit de leurs puissances également.
Pour que la somme des diviseurs de N soit impaire, il faut et il suffit que la somme de ses diviseurs impairs soit impaire donc que l’effectif de ses diviseurs impairs soit impair.
Or cet effectif est : (k1 + 1) x (k2 + 1) x (k3 + 1) x … (ki + 1).
Pour que ce produit soit impair, il faut et il suffit que tous ses facteurs soient impairs, donc que tous les k1, k2, k3 … ki soient pairs.
CQFD.
Démonstration 2 (la même, mais rédigée en langage courant) :
2 Rappels :
Tout nombre entier N peut s'écrire d’une façon et d'une seule comme un produit fini de nombres premiers différents à des puissances entières convenables (c'est la décomposition en facteurs premiers de ce nombre).
Ses diviseurs sont tous les entiers qui peuvent s'écrire comme des produits de ces facteurs premiers, chacun à une puissance pouvant varier de zéro jusqu’à celle qu'il a dans la décomposition.
Pour que la somme de tous les diviseurs de N soit impaire, il faut et il suffit que le nombre de ses diviseurs impairs soit impair.
Les diviseurs impairs de N sont tous les entiers qui peuvent s'écrire chacun comme un produit des facteurs premiers différents de 2 de la décomposition, chacun de ces facteurs étant à une puissance pouvant varier de 0 jusqu'à la valeur qu'elle a dans la décomposition.
Soit : a, b , c ... les valeurs des exposants des facteurs premiers différents de 2 de la décomposition.
Le nombre des diviseurs impairs de N est donc : (a + 1) x (b + 1) x (c + 1) ...
Pour que ce produit soit impair, il faut et il suffit que tous ces facteurs le soient.
Donc, il faut et il suffit que les exposants : a, b, c soient tous pairs.
Conclusion : pour que la somme de tous les diviseurs d'un nombre entier N soit impaire, il faut et il suffit que dans la décomposition en facteurs premiers de ce nombre entier, les facteurs premiers différents de 2 aient des puissances paires.
Démonstration 3 ( formulation plus rapide) :
Nous avons vu plus haut que :
Si N = aα x bβ x cγ ... avec : a, b, c, premiers tous différents,
Alors la somme de tous ses diviseurs vaut : (1 + a + a2 + a3 + .. + aα) x (1 + b + b2 + ... + bβ) x (1 + c + c2 + ... + cγ) x ....
Les diviseurs de N étant tous les termes du développement de ce produit.
Pour que ce produit soit impair, il faut et il suffit que chacun de ses facteurs le soit.
Si a, par exemple vaut 2, alors la somme des diviseurs de 2α qui vaut (1 + 2 + 22 + .... + 2α) est toujours impaire.
Pour les autres sommes qui sont les facteurs du produit : b , c , ... étant obligatoirement impairs, leurs puissances le sont aussi.
Les sommes : (1 + b + b2 + b3 + ... + bβ) , (1 + c + c2 + ... + cγ) , .... sont toutes impaires si et seulement si le nombre de termes de chacune l'est, donc si : b , γ ... sont des nombres pairs (ces sommes ayant respectivement β +1 , γ +1 , ... , termes).
On arrive à la même conclusion : pour que la somme de tous les diviseurs d'un nombre entier N soit impaire, il faut et il suffit que dans la décomposition en facteurs premiers de ce nombre entier, les facteurs premiers différents de 2 aient des puissances paires.
Remarque 2 : Calcul du nombre d'entiers inférieurs ou égaux à une valeur N ayant chacun la somme de tous leurs diviseurs impaire.
Nous allons voire que ce nombre vaut : Partie entière de racine carrée de (N) + Partie entière de racine carrée de (N/2)
Démonstration :
D'aprés la conclusion de la remarque 1, nous pouvons classer les entiers dont la somme de tous les diviseurs est impaire, en 2 classes disjointes sans en oublier :
Pour compter ceux qui sont inférieurs à un nombre N, il suffit de compter ceux appartenant à chacune des 2 classes et d'additionner les résultats.
Les carrés inférieurs ou égaux à N ont un éffectif de :
Partie entière de racine de (N)
Les nombres égaux au produit de 2 et d'un carré et qui sont inférieurs ou égaux à N, ont le même effectif que les carrés inférieurs ou égaux à (N/2). Cet effectif est :
Partie entière de racine de (N/2)
L'effectif des entiers inférieurs à N ayant chacun la somme de leurs diviseurs impaire est donc :
Partie entière de racine carrée de (N) + Partie entière de racine carrée de (N/2)
Extension 4 : Etant donnée une valeur N, cette extension permet de trouver tous les entiers S compris entre 2 bornes que l'on fixe et dont la somme des diviseurs est égale à N.
Extension 5 : Effectifs des nombres ayant la somme de leurs diviseurs d'une valeur S, pour S compris entre 2 limites.
Etant donne un intervalle [ L1 , L2 ].
Pour tout entier S de cet intervalle, il y a n nombres dont la somme des diviseurs vaut S.
Cette extension affiche par ordre croissant des valeurs de n les effectifs correspondants des valeurs de S situees dans l'intervalle.
Une option permet d'afficher les valeurs de S correspondant a chaque effectif.
Exemples avec ces 5 extensions :
Extension 1 : Liste de 1 à 80 des nombres avec leurs propriétés.
[Page 1]
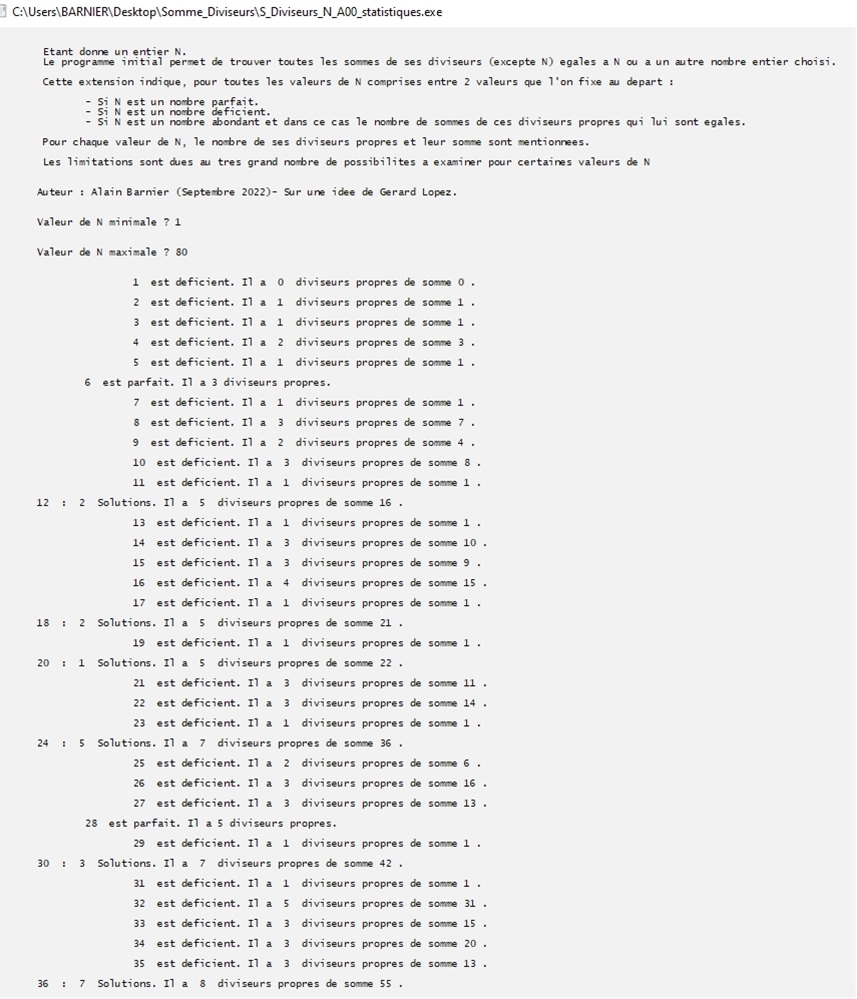
[Page 2] Suite
Extension 1 : Liste des nombres de 60 à 90 avec leurs propriétés
Extension 2 : Nombres abondants avec 0 solution et nombres parfaits, de 1 à 20 000
Remarque : le calcul se fige pour 17990. Il faudrait attendre trés longtemps pour obtenir la suite.
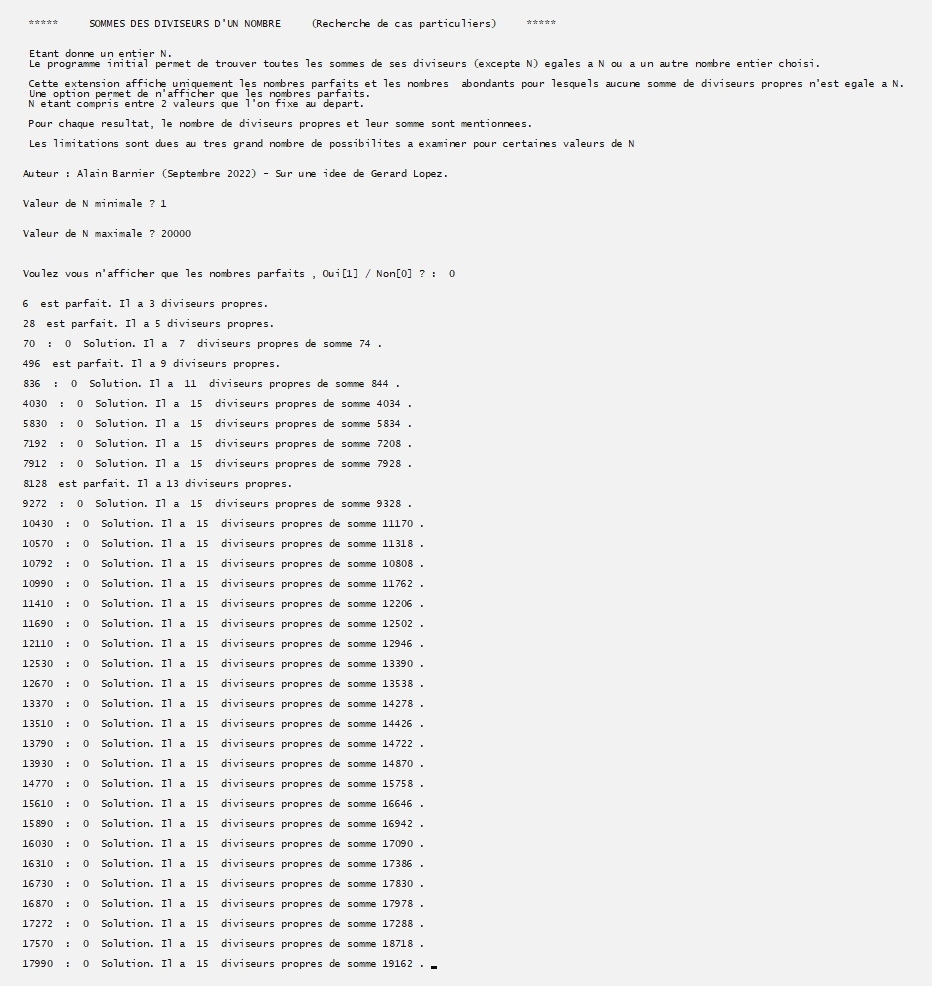
Extension 2 : Idem que précèdement mais seulement de 1 à 200,
puis seulement les nombres parfaits de 200 à 5000
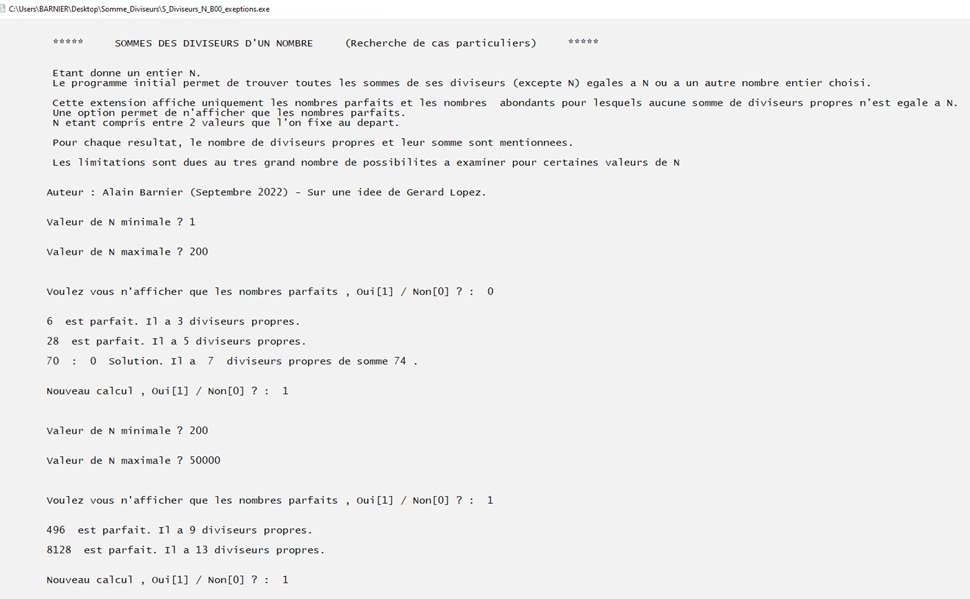
Extension 3 : Les exemples parlent d'eux mêmes.
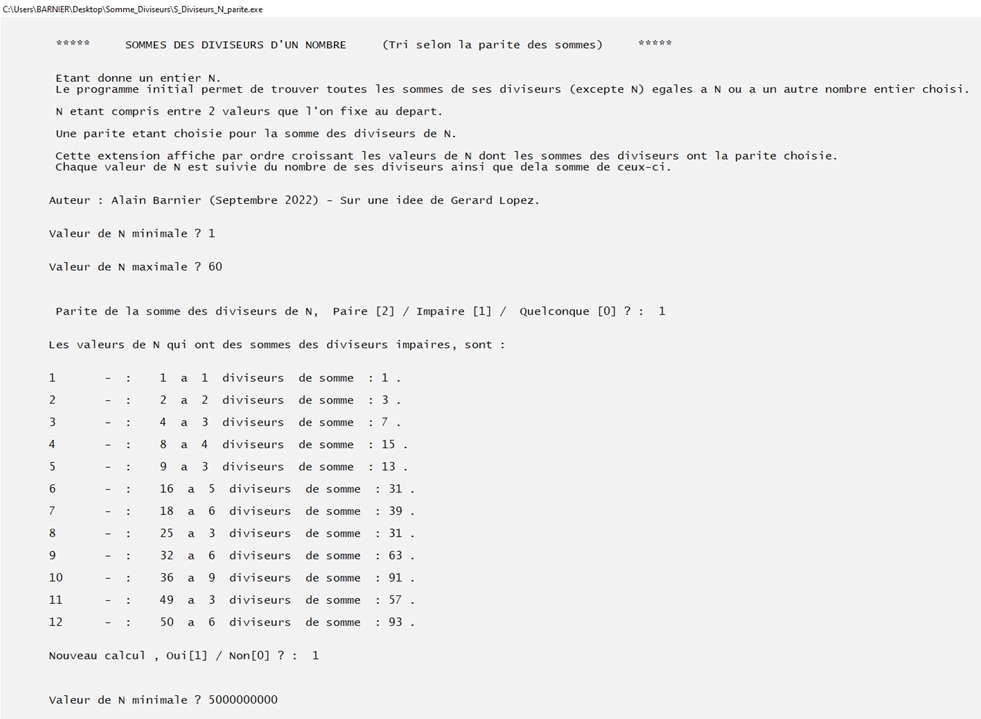
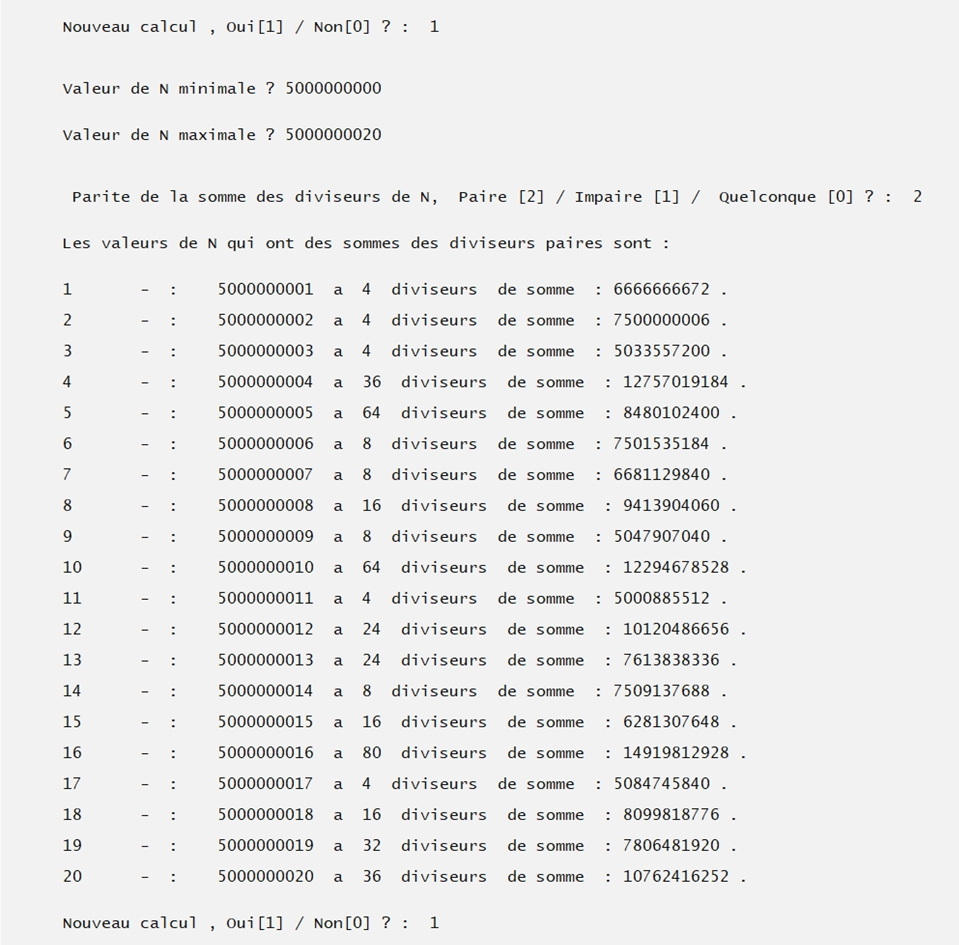
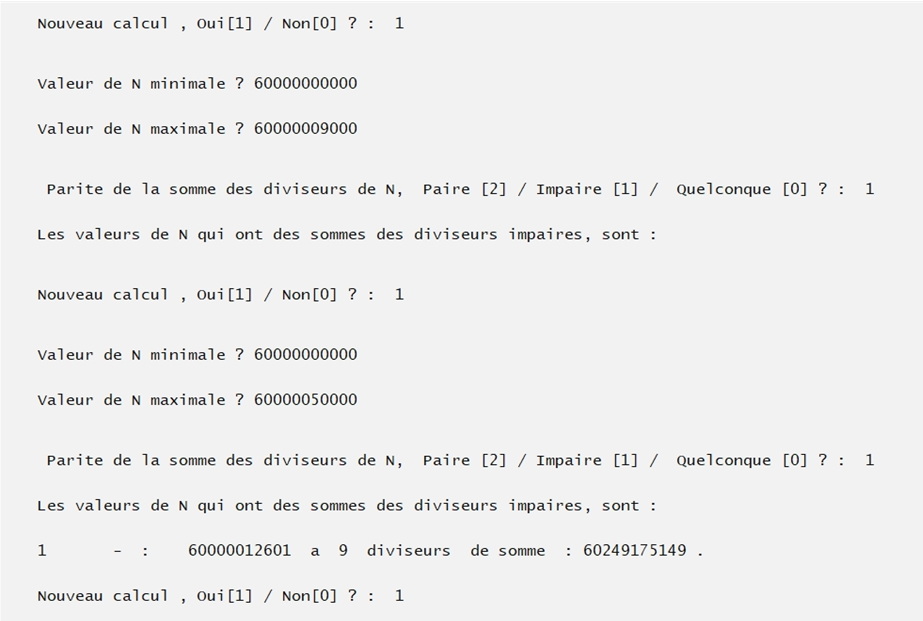
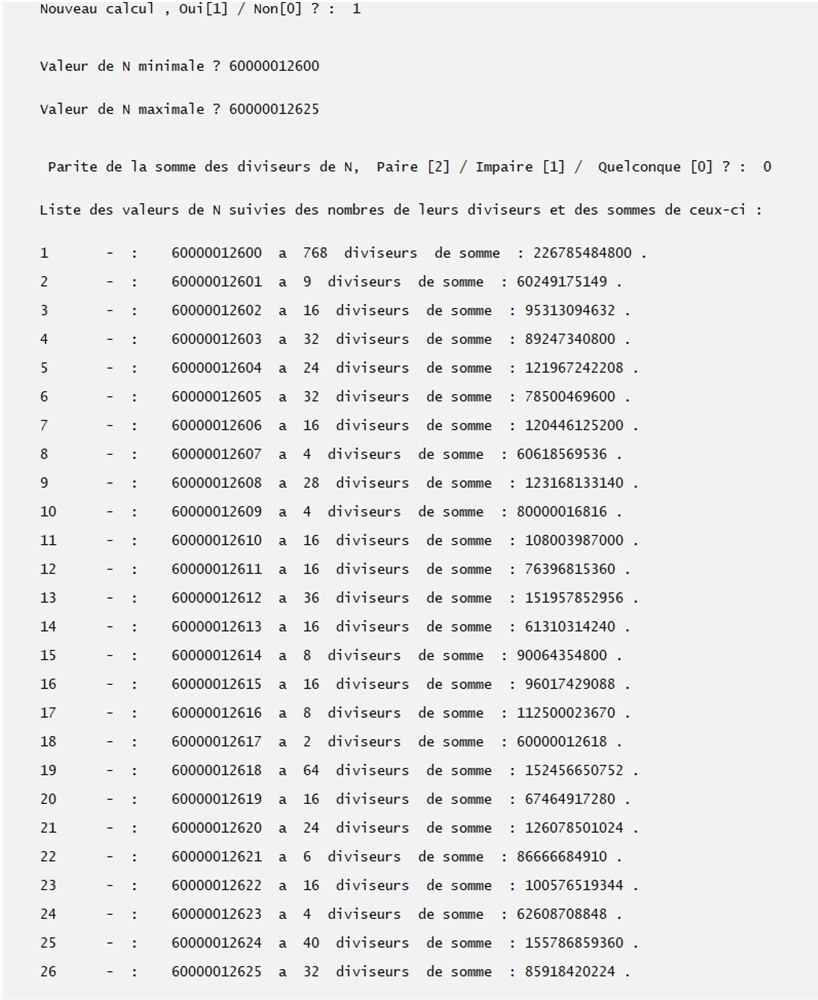
Extension 4 :
Extension 5
Téléchargement des versions A et B et des extensions :
Pour Windows :
N B : Windows fera peut-être des difficultés pour télécharger et/ou exécuter ces programmes. Il considère les extensions .exe comme étant celles de fichiers exécutables potentiellement dangereux . Il suffit de passer outre grace aux boites de dialogue contextuelles.
&
********************
&
&
&
&
Pour Linux :
Lire les instructions ci-dessous pour pouvoir faire fonctionner ces programmes avec Linux. (*)
&
********************
&
&
&
&
(*) Avec Linux :
Linux ne permet pas d'ouvrir directement ces programmes. Il faut passer par la console du terminal. Vous trouverez ci-dessous la procédure à suivre pour pouvoir exécuter les programmes téléchargés sous Linux. La compilation et les tests ont été faits avec la distribution d'UBUNTU.
Procédure permettant de faire fonctionner les programmes téléchargés sous Linux :
– D'abord, télécharger le programme.
– Le placer sur le bureau par exemple, ou dans un dossier de votre choix.
– Cliquez droit sur l'icone du programme, là ou il se touve. Choisir "propriétés" dans le menu contextuel, puis, sous l'onglet "permissions", côcher la case "autoriser l'éxécution du programme" (si cette case n'est pas déjà cochée).
– Ouvrir l'utilitaire Terminale (il se trouve dans le groupe Utility de la liste des programmes).
– Rentrez la commande /chemin du programme complet/Nom du programme , ou alors ./chemin relatif/nom du programme (le chemin relatif par du répertoire par défaut ou de celui dans lesquel vous vous êtes placé avec la commande cd ). Si vous vous êtes placé dans le répertoire où se trouve le programme, tapez simplement ./nom du programme.
– Le programme devrait se lancer alors dans la fenêtre du terminal.
[ Une vidéo de démonstration est en cours d'élaboration ]
Quelques liens sur le sujet :
typede nombres: nombres semi-parfaits (free.fr)
collection de nombres, parfait, multiparfait, amiable, sociable (free.fr)
Nombre presque parfait — Wikipédia (wikipedia.org)
Nombre parfait — Wikipédia (wikipedia.org)
Nombres_parfaits.pdf (free.fr)
La beauté des nombres parfaits - Québec Science (quebecscience.qc.ca)