NOMBRES PREMIERS
Logiciel permettant de :
Lister et trier les nombres premiers - Décomposer un nombre en facteurs premiers.
Table des matières :
- Descriptions et caractéristiques.
- Article PDF de présentation de ce logiciel et sur ses applications pédagogiques possibles.
- Remarques sur les nombres jumeaux et généralisation (actualisées le 26/10/2023).
- Propriétés et curiosités du nombre 31 par Gérard Lopez. (PDF)
- Téléchargements (Windows et Linux).
- Vidéo de démonstration. (Provisoire)
- Code des différentes versions.
- Autres programmes du même auteur :
Ces programmes permettent de :
1) Calculer, lister et/ou afficher les nombres premiers de différentes façons.
2) Décomposer en facteurs premiers n'importe quel nombre entier.
Les nombres premiers doivent être inférieurs à (263-1)*.
Les nombres à factoriser peuvent-être quelconques tant que leurs facteurs premiers ne dépassent pas (263-1) .
Mais les limitations sont surtout dûes aux temps de calcul des grands nombres premiers.
Sauf pour les décompositions en facteurs, tous les nombres premiers sont affichés avec leur rang.
Ces programmes permettent de calculer et afficher tous les nombres premiers jusqu'à une valeur ou un rang donné. On peut choisir de n'afficher que le dernier ou le plus grand de ces nombres. Ces nombres calculés sont tous mémorisés.
On peut afficher des nombres premiers isolés déjà calculés ou des séquences de ceux-ci en les triant grace à leurs rangs ou leurs valeurs.
Parmi les nombres déjà calculés, une option permet d'afficher et de compter tous les couples de nombres premiers consécutifs compris entre 2 valeurs et dont la différence a une valeur fixée [ Exemples ]. On peut choisir de ne faire afficher que les occurences pour lesquelles un nombre donné de solutions se suivent [ Remarque sur les nombres jumeaux et généralisation ].
La saisie des données est sécurisée : une entrée incompatible est re-demandée et ne provoque pas un "plantage".
Ces programmes sont fait pour des PC 64 bits. Ils sont téléchargeables ci-dessous.
Ils existent en 4 versions, identiques quand à leur fonctionement et leur présentation :
La version A :
Elle n'utilise que la mémoire vive de l'ordinateur. Elle est trés "portable" et convient pour calculer trés rapidement des nombres premiers jusqu'à des valeurs de 15 ou 20 millions et pour factoriser rapidement des nombres de 14 chiffres. Elle factorise aussi rapidement n'importe quel nombre ne comportant pas de facteurs de plus de 7 chiffres.
La version B1 :
Cette version utilise à la fois la mémoire vive de l'ordinateur et un fichier "liste.txt" contenant une grande quantité de nombres premiers. Cette version du programme ne peut pas compléter ce fichier avec de nouveaux nombres premiers mais elle peut les calculer et les stocker en mémore vive.
Elle permet de calculer rapidement des nombres premiers jusqu'à des valeurs de 3 milliards et factoriser rapidement des nombres de 18 chiffres. Elle factorise aussi rapidement n'importe quel nombre ne comportant pas de facteurs de plus de 9 chiffres.
Le fichier "liste.txt" contient les nombres premiers jusqu'au cent cinquante millionième. Il doit-être placé dans le même repertoire que le programme. Il ne sert qu'en lecture seule.
Son utilisation permet d'afficher et charger en mémoire vive, trés rapidement, les nombres premiers jusqu'au cent cinquante millionième *. Quand cette limite est dépassée, les nombres sont calculés et rajoutés à la liste en mémoire vive.
Une fois le programme fermé, les nombres premiers mémorisés en mémoire vive sont éffacés.
Le fichier "liste.txt" pèse 1,5 Go environ. Le programme et son fichier occupe donc un peu de place.
La version B2 :
Cette version utilise à la fois la mémoire vive de l'ordinateur et un fichier "liste2.txt" contenant une grande quantité de nombres premiers. Le programme peut compléter ce fichier ce qui permet d'étendre ces possibilités.
Cette version avec ses fichiers d'origine convient pour calculer rapidement des nombres premiers jusqu'à des valeurs de 3 milliards et pour factoriser rapidement des nombres de 18 chiffres. Elle factorise aussi rapidement n'importe quel nombre ne comportant pas de facteurs de plus de 9 chiffres.
Le fichier "liste2.txt" est couplé avec le fichier "NN2.txt". Ils sont tous les deux en lecture et écriture. Le premier contient les nombres premiers jusqu'au cent cinquante millionième *, le deuxième contient seulement l'effectif du premier. Ces fichiers doivent-être placés dans le même repertoire que le programme.
Leur utilisation permet d'afficher et charger en mémoire vive, trés rapidement, les nombres premiers jusqu'au cent cinquante millionième * (et même au-delà si "liste2.txt" a été complété lors des calculs précèdents). Quand on dépasse la dernière valeur du fichier, les nombres sont calculés et rajoutés à la liste en mémoire vive et les fichier "liste2.txt" et "NN2.txt" complétés ou mis à jour.
Une fois le programme fermé, les nombres premiers mémorisés en mémoire vive sont éffacés.
Le fichier "liste2.txt" pèse 1,5 Go environ. Le programme et son fichier occupent donc un peu de place.
La version C :
Cette denière version n'utilise pas la mémoire vive de l'ordinateur mais un fichier "liste1.txt" contenant une grande quantité de nombres premiers. Le programme peut le compléter pour un usage dans des calculs ultérieurs.
Cette version avec ses fichiers d'origine permet de calculer rapidement des nombres premiers jusqu'à des valeurs de 3 milliards et de factoriser rapidement des nombres de 18 chiffres. Elle factorise aussi rapidement n'importe quel nombre ne comportant pas de facteurs de plus de 9 chiffres. Elle est un peu plus lente que la B2.
Le fichier "liste1.txt" est accompagné du fichier "NN1.txt". Ils sont tous les deux en lecture et écriture. Le premier contient les nombres premiers jusqu'au cent cinquante millionième *, le deuxième contient seulement l'effectif du premier et la valeur de son dernier nombre. Ces fichiers doivent-être placés dans le même repertoire que le programme.
Leur utilisation permet d'afficher trés rapidement les nombres premiers jusqu'au cent cinquante millionième * (et même au-delà si "liste1.txt" a été complété lors des calculs précèdents). Quand on dépasse la dernière valeur du fichier, les nombres sont calculés et les fichiers "liste1.txt" et "NN1.txt" complétés ou mis à jour.
Le fichier "liste1.txt" pèse 1,5 Go environ. Le programme et son fichier occupent donc un peu de place.
Les versions B1 et C ont comme avantage que leurs fichiers annexes peuvent-être complétés, avec comme inconvénient le risque de les corrompre en interrompant un calcul en cours.
Pour palier à ce risque il est conseillé d'en faire une sauvegarde dans un autre répertoire.
Si l'on a pas fait de sauvegarde, il faut savoir qu'en cas d'absence d'un des deux fichiers ou des deux, les programmes les recrée en les initialisant vides tous les deux. Ils seront alors remplis au fur et à mesure des utilisations des programmes. Donc en cas de corruption d'un fichier, on peut en supprimer un des deux et ainsi on repartira à zéro.
* (263-1) ~ 9 milliards de milliards = 9 000 000 000 000 000 000.
* Le cent cinquante millionième nombre premier vaut : 3 121 238 909.
NB : L'intéret de mémoriser les nombres premiers calculés pour la version A est montré par cet exemple :
Quand, au premier lancement du programme A, on factorise :
101101101101101101101101101 (101, 9 fois) , il faut 1 minute pour afficher la solution :
(3)^2 x (101) x (757) x (333667) x (440334654777631).
Mais si on refait par la suite cette décomposition ou si l'on fait une décomposition similaire, sans avoir arréter le programme, le calcul est immédiat.
Il est également immédiat si avant de faire cette décomposition pour la première fois on calcule le 1 500 000 ème nombre premier (23879519). Cela prend 1 minute mais ce n'est plus à faire pour la même session du programme.
On remarque que le carré du 1 500 000 ème nombre premier est supérieur au plus grand facteur premier de la décomposition.
Avec les versions B (1 et 2) et même C, le calcul est trés rapide, car les programmes n'ont pas à calculer les nombres premiers qui sont mémorisés dans les fichiers "liste.txt". Il faut simplement quelques secondes pour les charger en mémoire à partir de ces fichiers. Ce n'est plus à le faire pour les calculs suivants tant qu'on ne ferme pas les programmes.
Remarques sur les nombres jumeaux et généralisation :
Les couples de nombres jumeaux sont toujours isolés (il ne peut pas y avoir 3 nombres premiers consécutifs qui différent de 2, à l'exeption de 3,5,7).
En effet sur 3 nombres qui se suivent avec des différences de 2, il y en a toujours un qui est un multiple de 3.
Proposition 1 : Plus généralement, on va démontrer que sur 3 nombres qui se suivent avec des différences égales de la forme 2n, un de ces 3 nombres est toujours un multiple de 3.
Les nombres entiers sont tous de la forme : 3k ou 3k+1 ou 3k+2.
1- Si le premier des 3 nombres est de la forme 3k, la vérification est faite. il n'est pas premier (sauf s'il s'agit de 3 lui même).
2 - Si le premier est de la forme 3k+1, le suivant est de la forme 3k+1+2n est le dernier 3k+1+2n+ 2n
On peut transformer l'écriture des 2 derniers de la façon suivante : 3k+3+2n -2 est le dernier 3k+3+2*2n-2.
soit 3(k+1) + 2(2(n-1)- 1) et 3(k+1) + 2(2n-1).
Dans ces 2 expressions, un des 2 exposants de 2, (n-1) ou n est obligatoirement paire, donc de la forme 2p.
Le nombre correspondant à cet exposant paire s'écrit donc : 3(k+1) + 2(22p - 1), soit encore 3(k+1) + 2(4p-1) et encore 3(k+1) + 2(4-1)(4(p-1) + 4(p-2) + .... + 1)
Finalement il s'écrit : 3(k+1) + 2*3(4(p-1) + 4(p-2) + .... + 1), c'est donc un multiple de 3.
3 - Si le premier est de la forme 3k+2, le suivant sera de la forme 3k+ 2 + 2n et le troisième de la forme 3k +2 + 2n + 2n.
ces 2 derniers nombres peuvent s'écrire : 3(k+1) + (2n -1) et 3(k+1) + (2(n+1) - 1).
En remarquant qu'un des 2 exposants de 2, n ou n+1 est obligatoirement paire de la forme 2p, le nombre qui le contient peut s'écrire :
3(k+1) + (22p - 1), soit encore 3(k+1) + (4p - 1) et finalement 3(k+1) + (4 - 1)(4(p-1) + 4(p-2) + ... + 1) = 3(k+1) + 3(4(p-1) + 4(p-2) + ... + 1).
Ce nombre est donc un multiple de 3.
La proposition est donc démontrée.
Il est donc vain de chercher des triplets de nombres premiers, consécutifs ou non, dont les éléments se suivent avec une différence constante de 2 (ou de 4 ou de 8 ou de ....2n en général). Les triplets commençant sont une exception.
On va démontrer une propriété plus générale englobant la précèdente.
Proposition 2 : Plus généralement encore, on va démontrer que sur 3 nombres qui se suivent avec une différence constante qui n'est pas un multiple de 3, un de ces 3 nombres est toujours un multiple de 3.
Les nombres entiers sont tous de la forme : 3k ou 3k+1 ou 3k+2.
1 - Si le premier des 3 nombres est de la forme 3k, la proposition est vérifiée.
2 - Si le premier est de la forme 3k+1 est que la différence constante entre les nombres est D, les 2 autres sont respectivement de la forme :
3k +1 + D et 3k +1 + 2D, qui peuvent s'écrire : 3k + (D+1) et 3(k-1) + 2(D+2)
3 - Si le premier est de la forme 3k+2 est que la différence constante entre les nombres est D, les 2 autres sont respectivement de la forme :
3k +2 + D et 3k +2 + 2D, qui peuvent s'écrire : 3k + (D+2) et 3k + 2(D+1).
On voit que :
- dans les cas 2 et 3, si (D+1) est un multiple de 3, le 2em et le 3em nombre sont ausi respectivement des multiples de 3.
- dans les cas 2 et 3, si (D+2) est un multiple de 3, le 3em et le 2em nombre sont ausi respectivement des multiples de 3.
Pour qu'aucun des 3 nombres ne soit un multiple de 3, il est donc nécessaire que la différence constante D soit tel que (D+1) et (D+2) ne soient pas des multiples de 3, donc que D soit un multiple de 3.
Si D n' est pas un multiple de 3 alors (D+1) ou (D+2) l'est et l'un des 3 nombres est un multiple de 3.
La proposition est donc démontrée.
Cette proposition démontre bien aussi la précèdente puisqu'aucune puissance de 2 n'est un multiple de 3.
Une conséquence.
La différence de 2 nombres premiers étant toujours paire et 3 étant le seul nombre premier divisible par 3 :
Il est vain de chercher des triplets de nombres premiers, consécutifs ou non, dont les éléments se suivent avec une différence constante qui n'est pas un multiple de 6. Les triplets commençant par 3 sont une exception.
Y a t'il une limite au nombre de nombres premiers consécutifs espacés régulièrement ?
Démontrons d'abord la proposition :
Si (N + 1) nombres entiers régulièrement espacés le sont d'un espace commun égal à N, l'un au moins est un multiple de (N + 1).
Si a est le premier de ces nombres les N suivants seront : (a + N), (a + 2*N), (a + 3*N), ... ,(a + N*N).
Divisons a par (N + 1) : a = k*(N + 1) + r ou r est un entier inférieur ou égal à N.
Un des N +1 entiers est donc de la forme (a + r*N). Comme a = k*(N + 1) + r, il est de la forme : k*(N +1) + r + r*N
Soit de la forme : k*(N + 1) + r*( N + 1).
Ce nombre est donc divisible par (N + 1).
Si nous envisageons le cas d'une suite de (N + 1) nombres consécutifs espacés réguliètement de N, dont on voudrait démontrer l'impossibilité qu'ils soient tous premiers.
Pour finir de démontrer qu'au moins un de ces N + 1 nombres n'est pas premier, il nous reste à envisager le cas ou le nombre divisible par (N + 1) de la proposition précèdente est égale à (N + 1). Ce dernier pourrait-être premier.
Dans ce cas on a : k*(N + 1) + r *(N + 1) = (N + 1) ou encore (k + r)*(N + 1) = (N + 1)
Ce qui n'est possible que si (k + r) = 1 soit : (k =1 et r = 0) ou (k = 0 et r = 1).
Comme le premier nombre vaut : a = k*(N + 1) + r, cela n'est possible que si ce premier nombre vaut (N + 1) ou 1.
S'il vaut 1, 1 n'est pas premier.
(on peut aussi dire plus simplement que si (N + 1) fait partie de la suite, ce ne peut-être que son premier terme).
S'il vaut (N + 1) la suite des (N + 1) nombres serait : N +1 , 2N +1 , 3N + 1 , 4N + 1 , ... , (N - 2)*N + 1 , (N - 1)*N + 1 , N*N + 1 , (N + 1)*N + 1.
Avec parmi eux : (N - 2)*N +1 = N^2 - 2N + 1 = (N -1)^2, qui n'est pas premier.
Donc dans ce cas la suite des (N + 1) nombres, contient aussi un nombre non premier.
Il en résulte que :
Comme nous avons vu que des nombres premiers régulièrement espacés ne peuvent l'être que d'un espace commun multiple de 6 (sauf pour les triplets commençant par 3), il en résulte que nous chercherions vainement k*6 + 1 nombres premiers régulièrement espacés du même espace égal à k*6 (consécutifs ou non). Le nombre de nombres premiers consécutifs ou non, régulièrement espacés de k*6 est donc majoré par k*6.
.
La différence entre 2 nombres premiers consécutifs est-elle limitée ?
Nous allons voir que non !
En effet, considérons le nombre N!
Les (N - 1) nombres qui le suivent directement aprés avoir omis (N! +1), qui sont : (N! + 2), (N! + 3), (N! + 4), (N! + 5 ),... (N! + (N - 1)), (N! + N), sont chacun divisibles respectivement par : 2, 3, 4, 5, ... , (N - 1), N. Ils ne sont donc pas premiers.
Nous pouvons donc construire des suites finies de nombres entiers consécutifs, dont aucun n'est premier, aussi longues que nous voulons.
La différence de 2 nombres premiers consécutifs n'est donc pas majorée.
Rappelons tout de même que l'effectif des nombres premiers ne l'est pas non plus.
Pour plus de renseignements sur ce sujet, consultez par exemple l'article sur cette question de Wikipédia.
Calculs enchainés :
1) On commence par décomposer 3 nombres en facteurs premiers :
Le dernier nombre premier qui a été calculé pour les décompositions est 1531, c'est le 242 e.
2) Sans fermer le programme, on calcule et affiche le nombre premier suivant immédiatement inférieur à 2500 (on tape =-2500 comme valeur de K). C'est 2477.
Pour le determiner le programme à dû calculer celui qui le suit : 2503, c'est le 368 e.
3) On affiche ensuite les 32 nombres premiers suivants (on tape 32 comme valeur de K).
Ils sont affichés avec leurs rangs du 369 e jusqu'au 400 e.
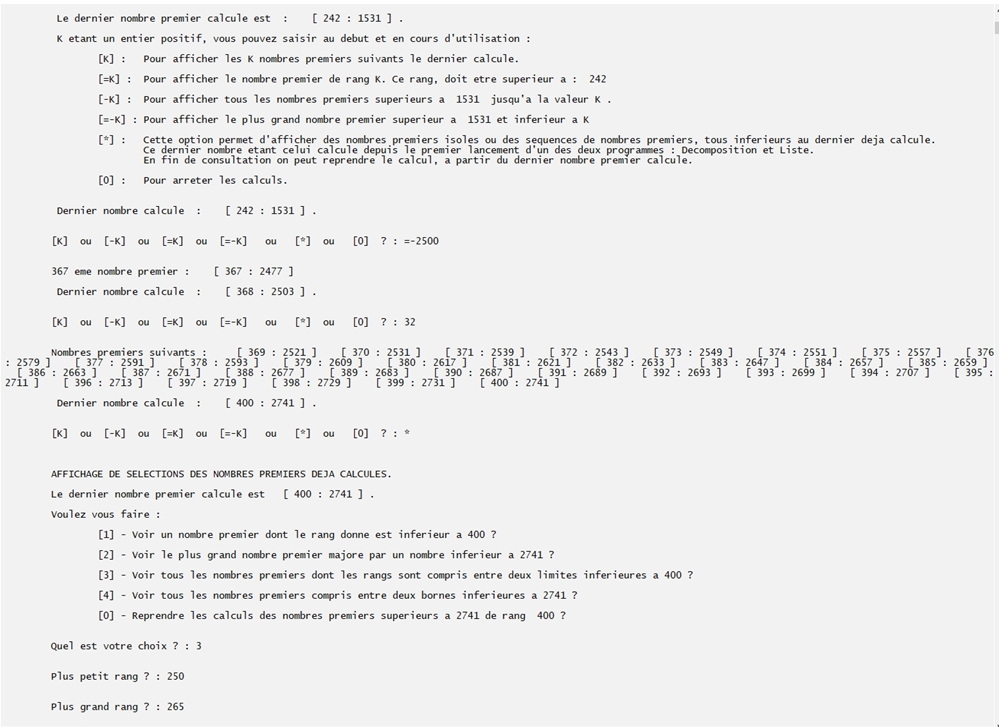
Pour les calculs précèdents, le programme a calculé et mémorisé les nombres premiers jusqu'à 2741, le 400 e.
4) Sans fermer le programme, en tapant * comme valeur de K, on peut lui demander de nous afficher avec leurs rangs les nombres premiers du 250 e au 265 e.
5) Puis on reprend le calcul de nouveaux nombres et on lui demande d'afficher le 1000 e (on tape =1000, comme valeur de K) : 7919.
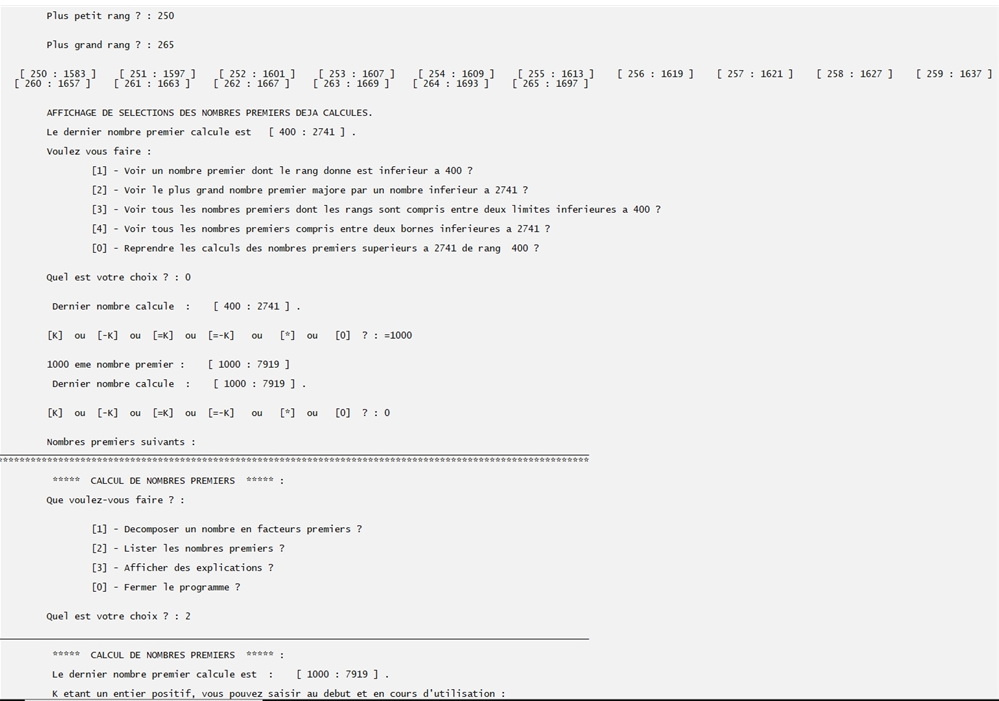
On ferme le programme.
________________________________________________________________________________________________________________
Calculs de nombres premiers de rangs élevés : 100 000 e et 1 000 000 e.
Pour ces valeurs, avec la version basique A, les calculs sont encore rapides.
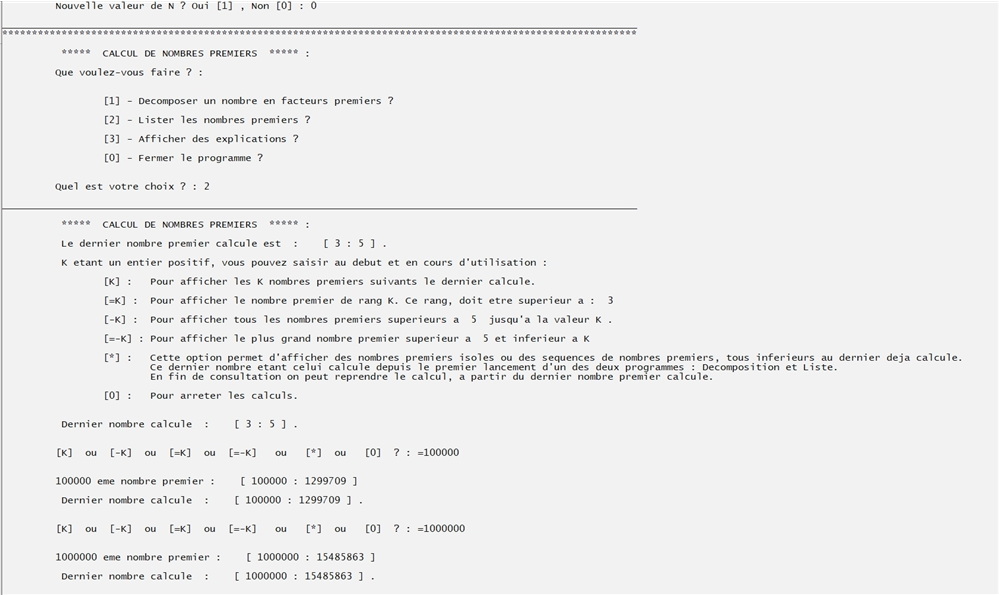
Décompositions en facteurs premiers de grands nombres.
Tant que les facteurs premiers restent dans certaines limites, les décompositions sont rapides.
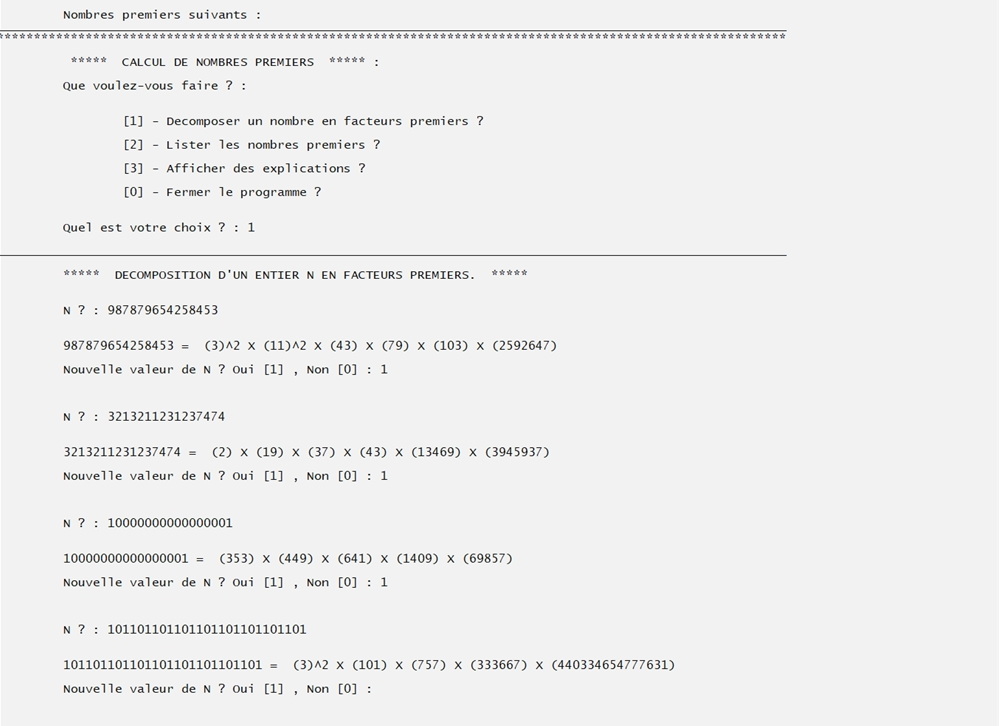
On peut décomposer des nombres entiers de trés grandes tailles grâce à l'utilisation de l'extension NTL du C++.
Ceci à condition que leurs facteurs premiers soient de dimensions convenables (voire mode d'emploie ci-dessus).
Pour la dernière valeur de cet exemple, les calculs sont trés longs avec la version A basique.
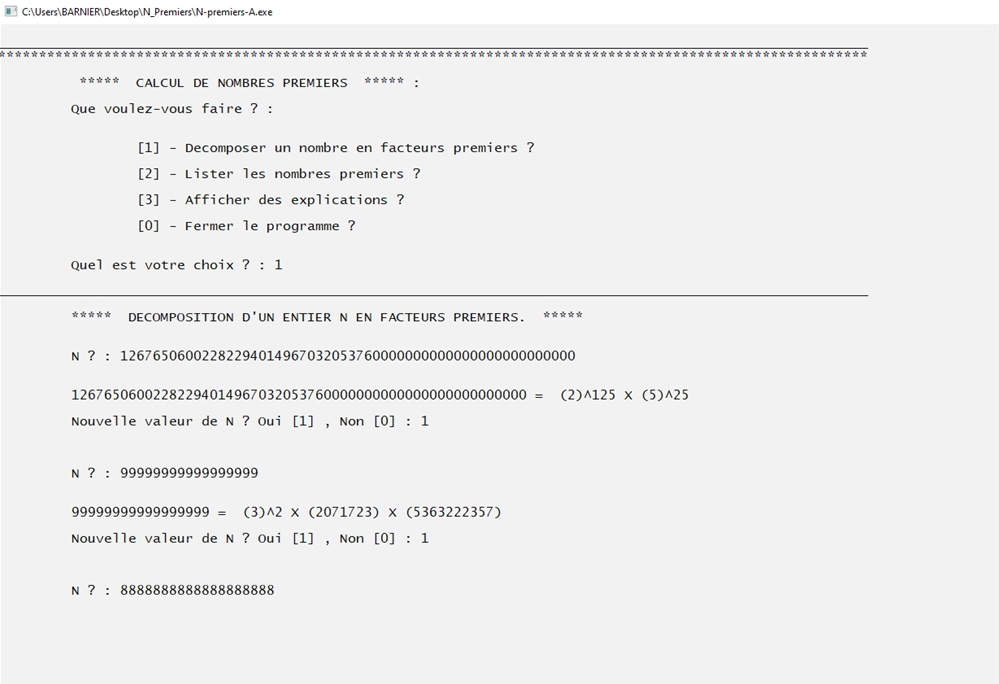
Ils ne prennent que quelques secondes avec la version B qui utilise un fichier préenregistré d'une grande quantité de nombres premiers :
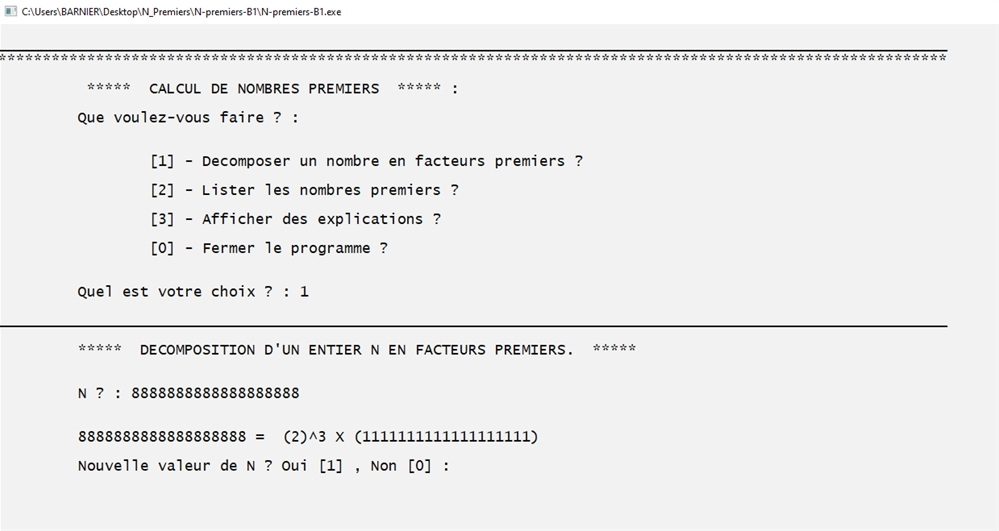
Avec cette version B, le programme ne met que quelques secondes pour afficher le cent millionième nombre premier :
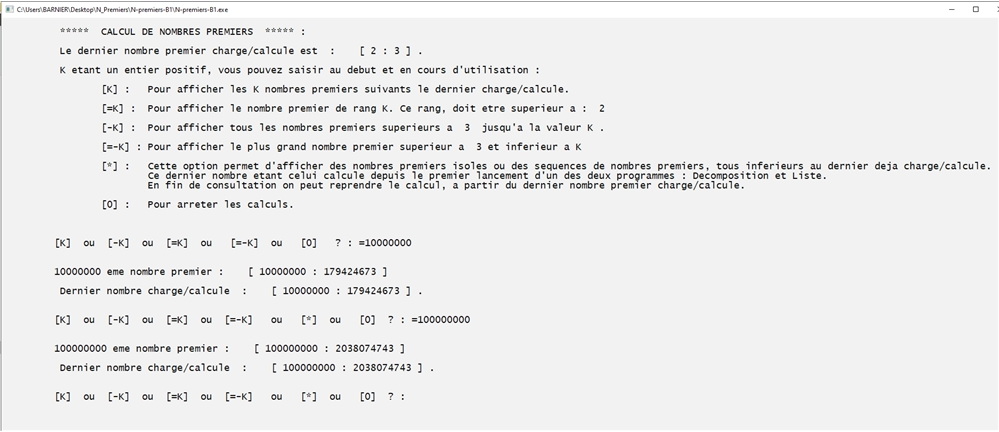
Recherche de Nombres premiers jumeaux ou voisins de différence donnée dans un intervalle :
Aprés avoir calculé les nombres premiers jusqu'au 100 000 e sans les afficher, on recherche les nombres jumeaux entre 1 et 500 puis les nombres consécutifs dont la différence est 30 entre 60 000 et 70 000.
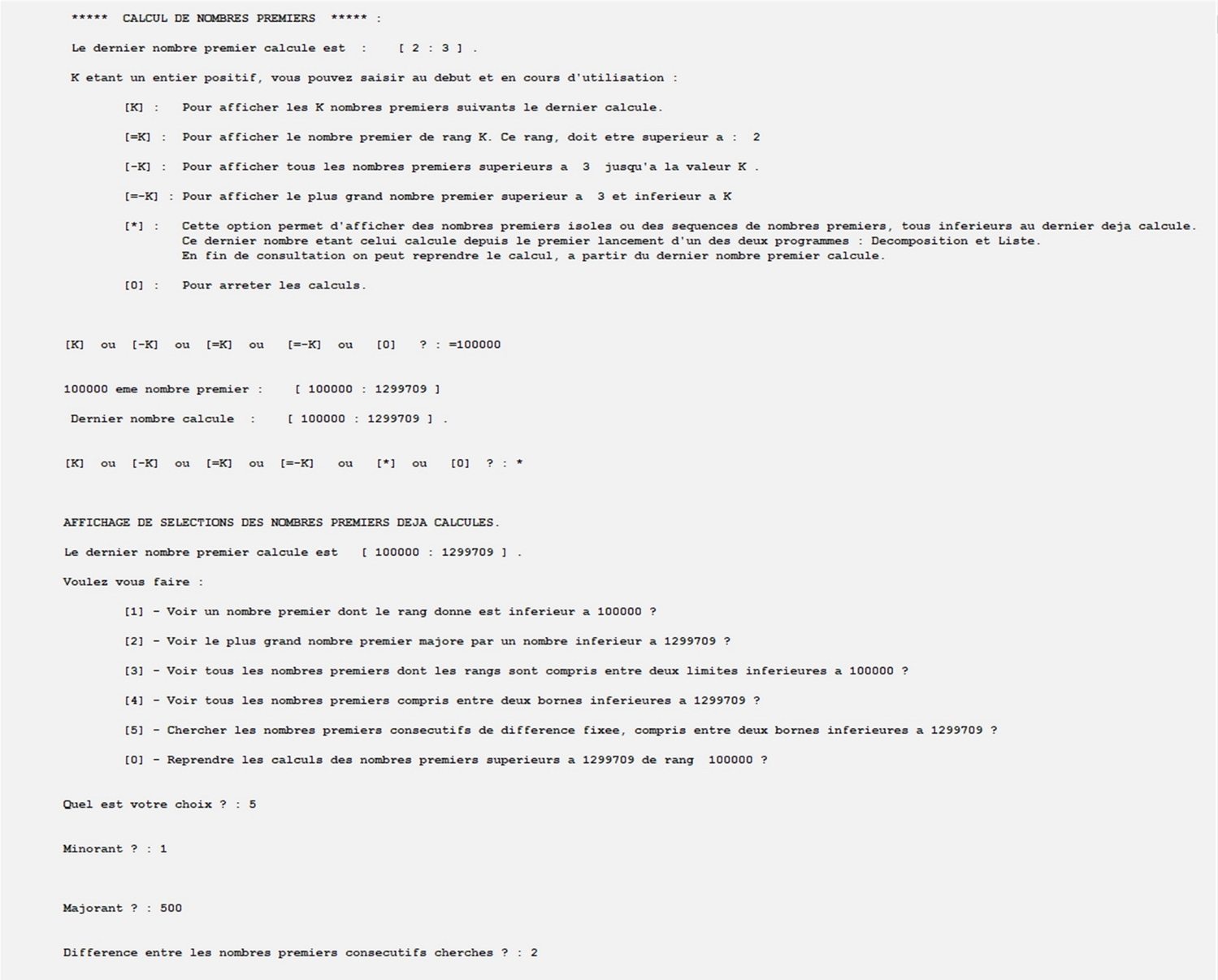
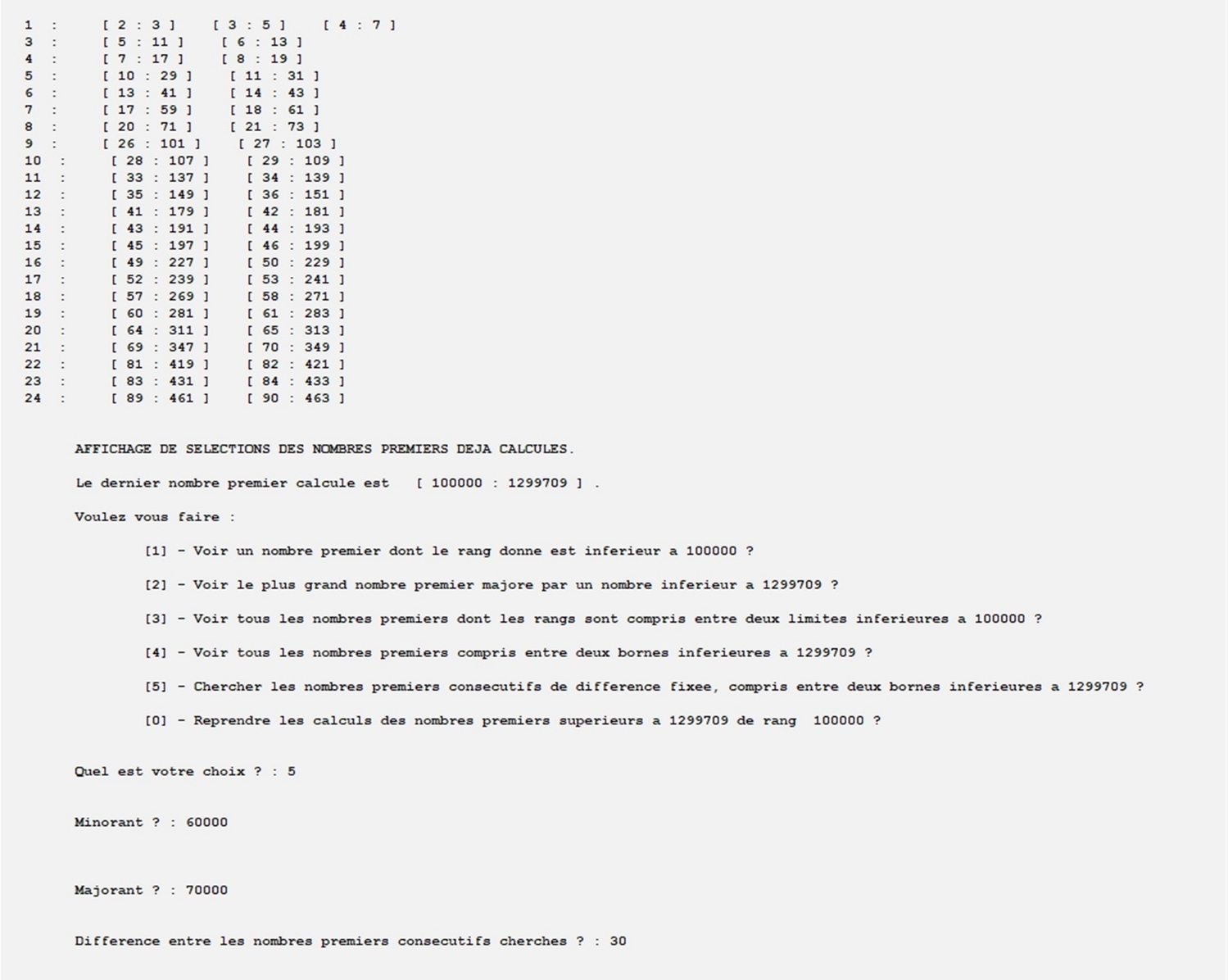
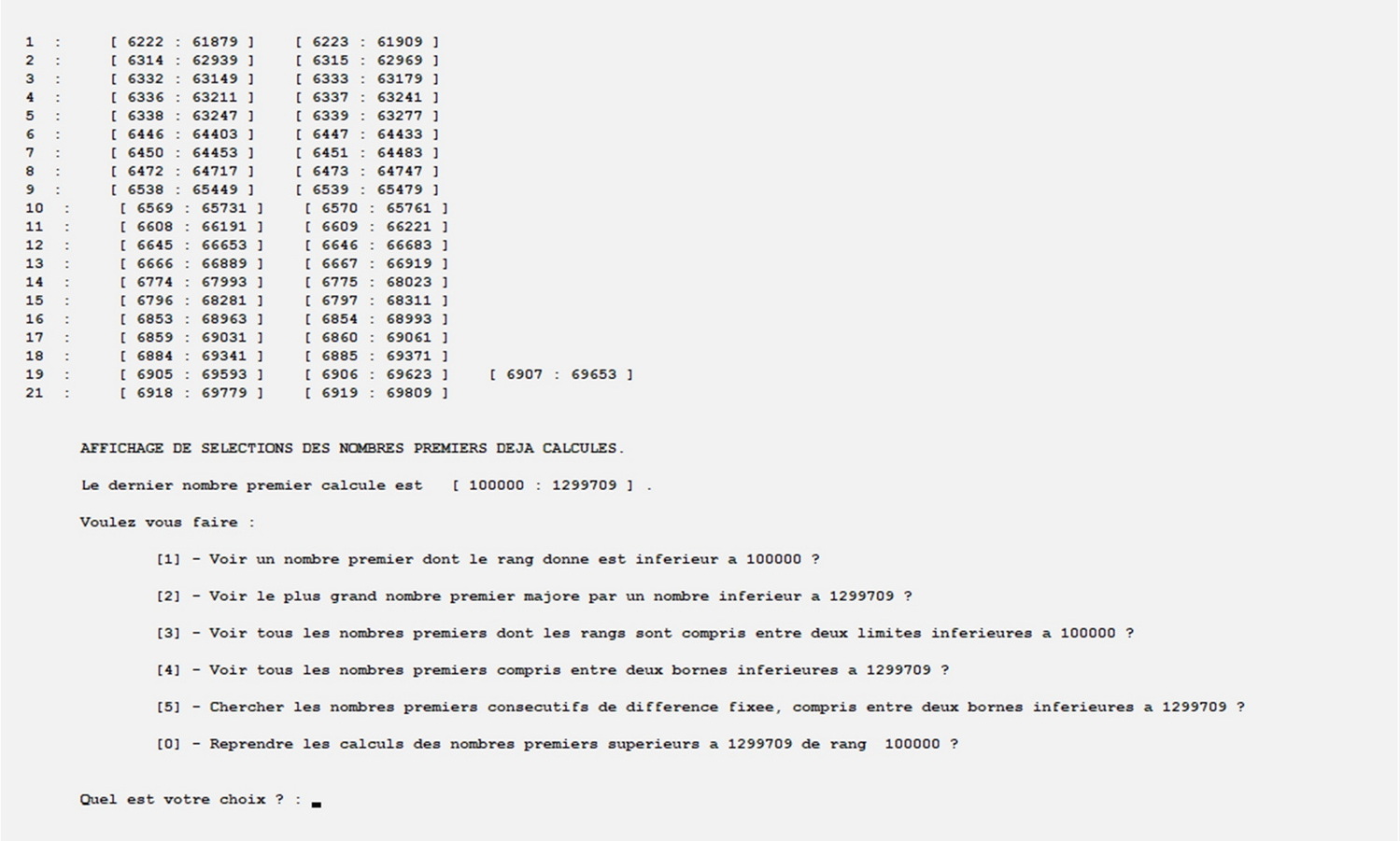
Utilisation de l'option qui permet de n'afficher que les solutions pour lesquelles un nombre donné de premiers consécutifs conviennent :
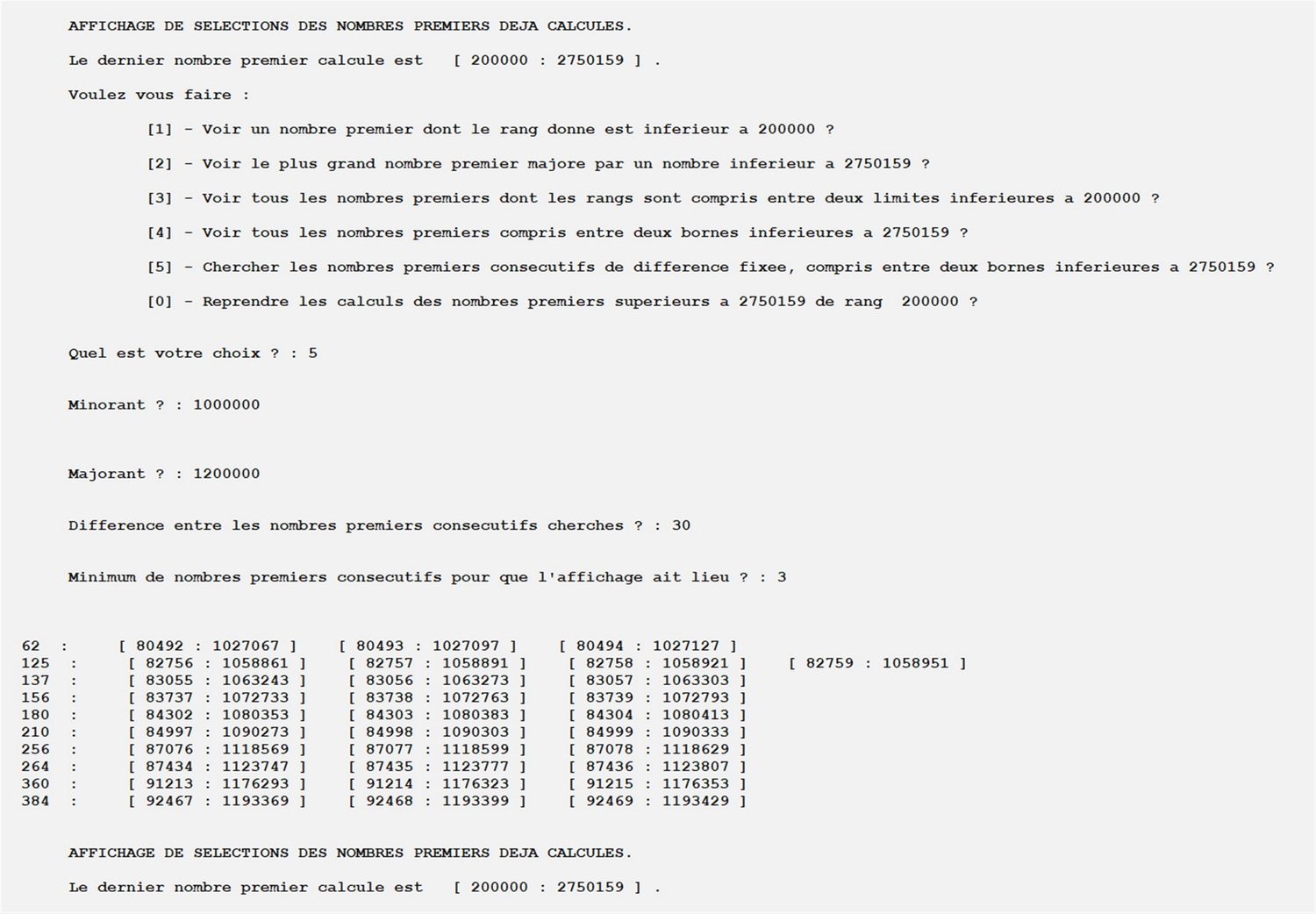
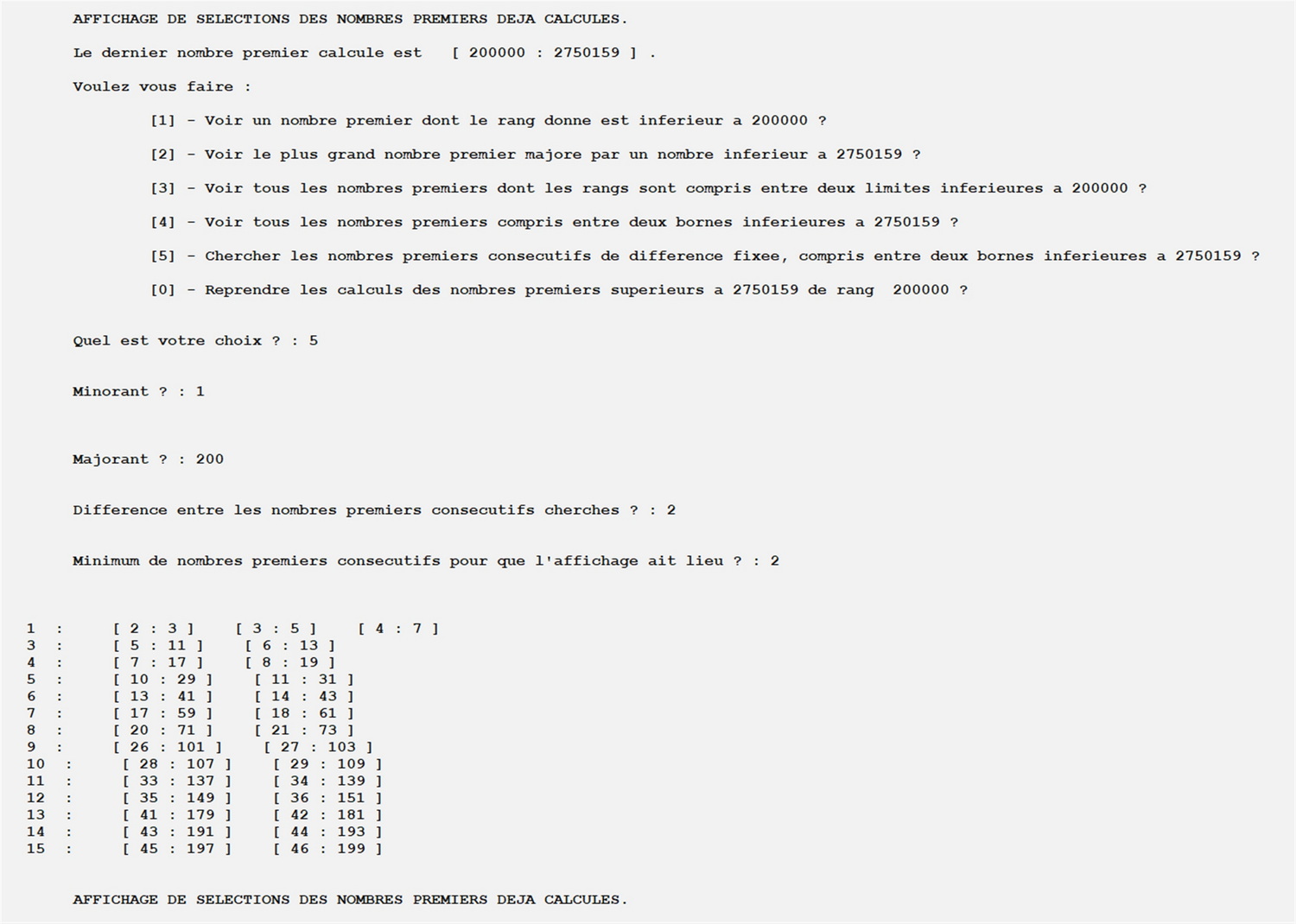
Particularité du progamme - Version C
Cette version n'utilise pas la mémoire vive pour stocker les nombres premiers calculés, mais elle utilise un fichier du disque dur contenant ces nombres jusqu'au 150 000 000 e. Ce fichier peut-être compléter selon les besoins.
Si l'on veut étudier des nombres premiers inférieurs, il faut choisir l'option * pour la valeur de K.
Cette option permet d'afficher des sélections de nombres premiers de la liste.
D'abord faisons afficher ceux situés entre les valeurs 2000 000 000 e et 2 000 000 050.
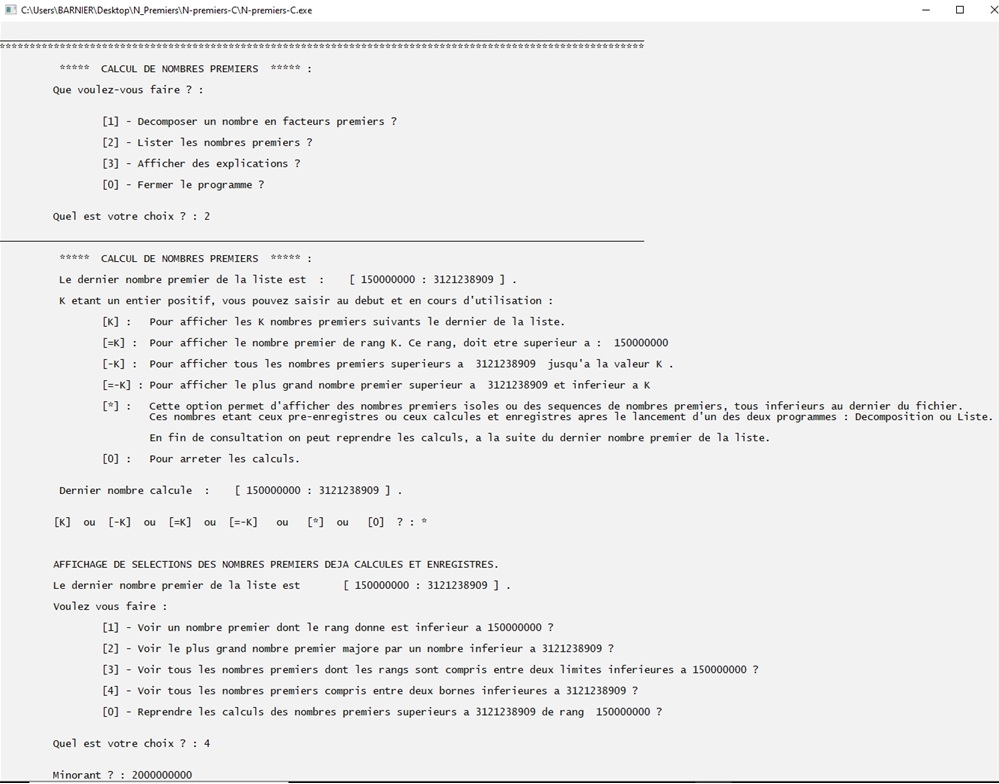
Il y en a 2 : le 98222288 e et le 98222289 e.
Vérifions que le 98222287 est plus petit que 2 000 000 000 et que le 98222290 e est plus grand que 2 000 000 050.
Calculons maintenant les 30 nombres premiers suivant le 150 000 000 e, dernier de la liste :
Il nous faudra rentrer 30 comme valeur de K.
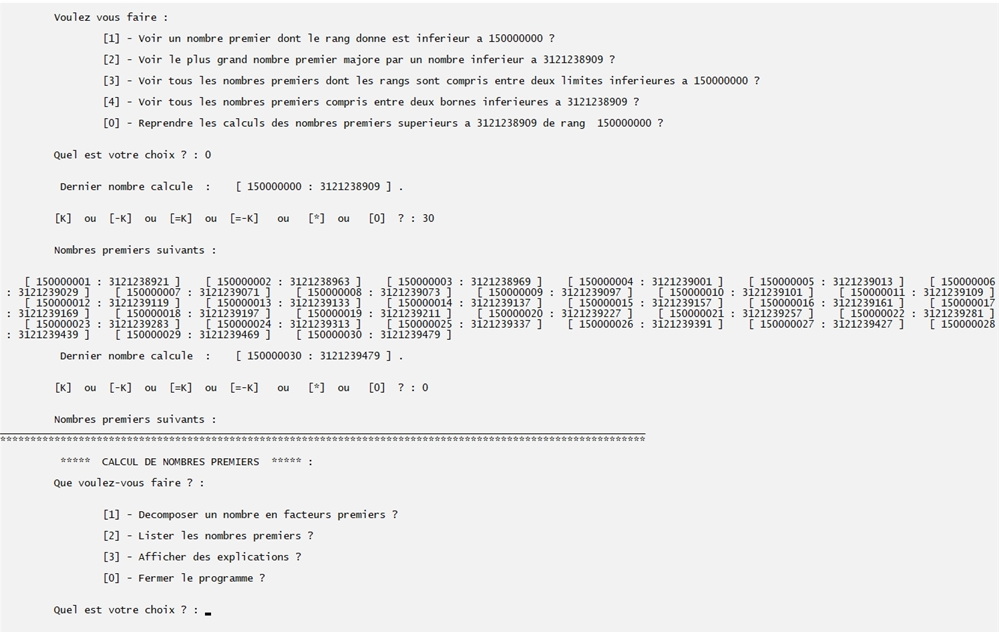
On peut vérifier que la liste du fichier a bien été complétée et se termine au 150 000 030 e nombre premier qui est : 3 121 239 479.
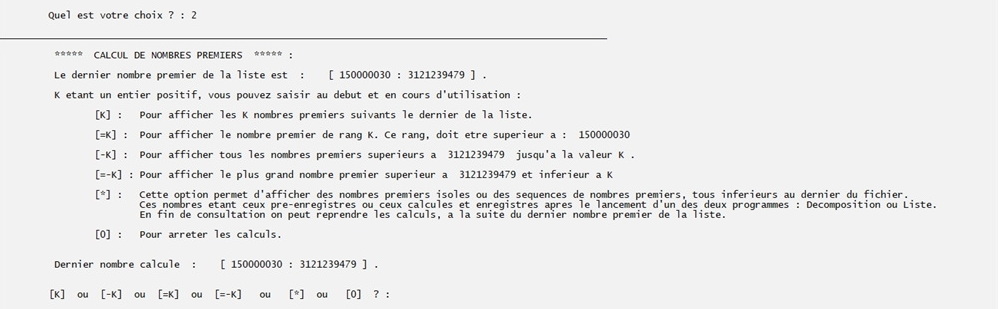
Ne pas interrompre le programme quand il calcule de nouvelles valeurs car celà peut corrompre le ficher enregistré sur le disque dur (voire le mode d'emploie).
Téléchargement des différentes versions.
Téléchargez les différentes versions à l'aide des liens suivants (Windows et Linux) :
Pour Windows :
Les programmes téléchargés s'ouvrent par défaut dans une console (petite fenêtre) qui a un fond noir. On peut facilement en modifier la dimension et la position à l'ouverture, ainsi que la couleur du fond et des écritures, la police et sa taille... en cliquant avec le bouton droit dans la barre du haut de cette console et en ouvrant la fenêtre des "propriétés" grace au menu contextuel qui apparait. Ces réglages resteront mémorisés pour les utilisations ultérieures.
· Version de base [du 01/05/2023] utilisant la mémoire vive seulement. Elle est moins volumineuse mais moins rapide pour les grands nombres premiers.
· Version qui utilise la mémoire vive et le fichier annexe "liste.txt" [version du 02/05/2023], en écriture seulement. Il contient les nombres premiers jusqu'au cent cinquante millionième. Au delà les nombres sont calculés mais le fichier n'est pas complété :
N-premiers-B1 (*)
· Version qui utilise la mémoire vive et les fichiers annexes "liste2.txt" et "NN2.txt" [version du 02/05/2023], en lecture et écriture. Le premier contient les nombres premiers jusqu'au cent cinquante millionième et peut-être complété au delà du cent cinquante millionième :
N-premiers-B2 (*)
· Version qui n'utilise pas la mémoire vive mais les fichiers annexes "liste1.txt" et "NN1.txt" [version du 14/08/2023], en lecture et écriture. Le premier contient les nombres premiers jusqu'au cent cinquante millionième et peut-être complété au delà du cent cinquante millionième :
N-premiers-C (*)
(*) Dossier compressé au format ZIP auto-extractible ( ~ 240 Mo) contenant le programme et son/ses fichiers annexes. Le programme et le/les fichiers annexes doivent toujours se trouver dans le même répertoire. Il est recommandé, surtout pour les versions .B2 et .C de faire une sauvegarde des fichiers annexes.
Pour Linux :
Lire les instructions ci-dessous pour pouvoir faire fonctionner ces programmes avec Linux.
Linux ne permet pas d'ouvrir directement ces programmes. Il faut passer par la console du terminal. Vous trouverez ci-dessous la procédure à suivre pour pouvoir exécuter les programmes téléchargés sous Linux. La compilation et les tests ont été faits avec la distribution d'UBUNTU.
Procédure permettant de faire fonctionner les programmes téléchargés sous Linux :
– D'abord, télécharger le programme.
– Le placer sur le bureau par exemple, ou dans un dossier de votre choix.
– Cliquez droit sur l'icone du programme, là ou il se touve. Choisir "propriétés" dans le menu contextuel, puis, sous l'onglet "permissions", côcher la case "autoriser l'éxécution du programme" (si cette case n'est pas déjà cochée).
– Ouvrir l'utilitaire Terminale (il se trouve dans le groupe Utility de la liste des programmes).
– Rentrez la commande /chemin du programme complet/Nom du programme , ou alors ./chemin relatif/nom du programme (le chemin relatif par du répertoire par défaut ou de celui dans lesquel vous vous êtes placé avec la commande cd ). Si vous vous êtes placé dans le répertoire où se trouve le programme, tapez simplement ./nom du programme.
– Le programme devrait se lancer alors dans la fenêtre du terminal.
· Version de base [du 01/05/2023] utilisant la mémoire vive seulement. Elle est moins volumineuse mais moins rapide pour les grands nombres premiers.
· Version qui utilise la mémoire vive et le fichier annexe "liste.txt" [version du 02/05/2023], en écriture seulement. Il contient les nombres premiers jusqu'au cent cinquante millionième. Au delà les nombres sont calculés mais le fichier n'est pas complété :
· Version qui utilise la mémoire vive et les fichiers annexes "liste2.txt" et "NN2.txt" [version du 02/05/2023], en lecture et écriture. Le premier contient les nombres premiers jusqu'au cent cinquante millionième et peut-être complété au delà du cent cinquante millionième :
· Version qui n'utilise pas la mémoire vive mais les fichiers annexes "liste1.txt" et "NN1.txt" [version du 14/08/2023], en lecture et écriture. Le premier contient les nombres premiers jusqu'au cent cinquante millionième et peut-être complété au delà du cent cinquante millionième :
(**) Dossier compressé au format ZIP ( ~ 380 Mo) contenant le programme et son/ses fichiers annexes. Le programme et le/les fichiers annexes doivent toujours se trouver dans le même répertoire. Il est recommandé, surtout pour les versions .B2 et .C de faire une sauvegarde des fichiers annexes. De plus, pour que le programme puisse utiliser le ou les fichiers annexes, il faut que le répertoire par défaut du terminal soit celui du répertoire dans lequel ces fichiers sont placés. Pour celà utiliser la commande cd du terminal : cd /chemin absolu complet du repertoire avant de lancer le programme par la commande : ./nom du programme .
Vidéo de démonstration (provisoire)